Unofficial Deep Learning Lecture 6 Notes
Hi All,
Should give some props to Jeremy for covering a lot of ground today. I could barely keep up. I’ll need your help filling in some of the blanks near the beginning and end of lecture. @jeremy could you wikify the post when you get a chance?
I’ll also go back and add all the diagrams for the CNN vs. RNN portion, will get to it later in the week. In the meantime, hoping that the notes help you guys out! Feel free to edit / add / patch what you can.
Tim
Review of Last week
Last week we made the collaborative filtering library from scratch.
In the learner.py file
CollaborativeFilterDataset Generator
class CollabFilterDataset(Dataset):
def __init__(self, path, user_col, item_col, ratings):
self.ratings,self.path = ratings.values.astype(np.float32),path
self.n = len(ratings)
(self.users,self.user2idx,self.user_col,self.n_users) = self.proc_col(user_col)
(self.items,self.item2idx,self.item_col,self.n_items) = self.proc_col(item_col)
self.min_score,self.max_score = min(ratings),max(ratings)
self.cols = [self.user_col,self.item_col,self.ratings]
@classmethod
def from_data_frame(cls, path, df, user_name, item_name, rating_name):
return cls(path, df[user_name], df[item_name], df[rating_name])
@classmethod
def from_csv(cls, path, csv, user_name, item_name, rating_name):
df = pd.read_csv(os.path.join(path,csv))
return cls.from_data_frame(path, df, user_name, item_name, rating_name)
def proc_col(self,col):
uniq = col.unique()
name2idx = {o:i for i,o in enumerate(uniq)}
return (uniq, name2idx, np.array([name2idx[x] for x in col]), len(uniq))
def __len__(self): return self.n
def __getitem__(self, idx): return [o[idx] for o in self.cols]
def get_data(self, val_idxs, bs):
val, trn = zip(*split_by_idx(val_idxs, *self.cols))
return ColumnarModelData(self.path, PassthruDataset(*trn), PassthruDataset(*val), bs)
def get_model(self, n_factors):
model = EmbeddingDotBias(n_factors, self.n_users, self.n_items, self.min_score, self.max_score)
return CollabFilterModel(to_gpu(model))
def get_learner(self, n_factors, val_idxs, bs, **kwargs):
return CollabFilterLearner(self.get_data(val_idxs, bs), self.get_model(n_factors), **kwargs)
def get_emb(ni,nf):
e = nn.Embedding(ni, nf)
e.weight.data.uniform_(-0.05,0.05)
return e
class EmbeddingDotBias(nn.Module):
def __init__(self, n_factors, n_users, n_items, min_score, max_score):
super().__init__()
self.min_score,self.max_score = min_score,max_score
(self.u, self.i, self.ub, self.ib) = [get_emb(*o) for o in [
(n_users, n_factors), (n_items, n_factors), (n_users,1), (n_items,1)
]]
def forward(self, users, items):
um = self.u(users)* self.i(items)
res = um.sum(1) + self.ub(users).squeeze() + self.ib(items).squeeze()
return F.sigmoid(res) * (self.max_score-self.min_score) + self.min_score
class CollabFilterLearner(Learner):
def __init__(self, data, models, **kwargs):
super().__init__(data, models, **kwargs)
self.crit = F.mse_loss
class CollabFilterModel(BasicModel):
def get_layer_groups(self): return self.model
from torch import nn
class EmbeddingNet(nn.Module):
def __init__(self, n_users, n_movies, nh=10, p1=0.05, p2=0.5):
super().__init__()
(self.u, self.m) = [get_emb(*o) for o in [
(n_users, n_factors), (n_movies, n_factors)]]
self.lin1 = nn.Linear(n_factors*2, nh)
self.lin2 = nn.Linear(nh, 1)
self.drop1 = nn.Dropout(p1)
self.drop2 = nn.Dropout(p2)
def forward(self, cats, conts):
users,movies = cats[:,0],cats[:,1]
x = self.drop1(torch.cat([self.u(users),self.m(movies)], dim=1))
x = self.drop2(F.relu(self.lin1(x)))
return F.sigmoid(self.lin2(x)) * (max_rating-min_rating+1) + min_rating-0.5
%reload_ext autoreload
%autoreload 2
%matplotlib inline
import sys
sys.path.append('../repos/fastai')
from fastai.learner import *
from fastai.column_data import *
path='ml-latest-small/'
ratings = pd.read_csv(path+'ratings.csv')
ratings.head()
val_idxs = get_cv_idxs(len(ratings))
wd=2e-4
n_factors = 50
movies = pd.read_csv(path+'movies.csv')
print(movies.shape, ratings.shape)
(9125, 3) (100004, 4)
cf = CollabFilterDataset.from_csv(path, 'ratings.csv', 'userId', 'movieId', 'rating')
learn = cf.get_learner(n_factors, val_idxs, 64, opt_fn=optim.Adam)
movie_names = movies.set_index('movieId')['title'].to_dict()
g=ratings.groupby('movieId')['rating'].count()
topMovies=g.sort_values(ascending=False).index.values[:3000]
topMovieIdx = np.array([cf.item2idx[o] for o in topMovies])
Bias
Each movie has its own bias.
To take a look at the layers of our PyTorch model.
m=learn.model; m
EmbeddingDotBias (
(u): Embedding(671, 50)
(i): Embedding(9066, 50)
(ub): Embedding(671, 1)
(ib): Embedding(9066, 1)
)
Layers require Variables because we need to keep track of the derivatives. The newest version of PyTorch will get rid of Variables, and it will all be native / built in. PyTorch engineering is moving towards the direction to be more Pythonic and closer to NumPy.
movie_bias = to_np(m.ib(V(topMovieIdx)))
EmbeddingDotBias (
(u): Embedding(671, 50)
(i): Embedding(9066, 50)
(ub): Embedding(671, 1)
(ib): Embedding(9066, 1)
)
Let’s check one of the variables
m.ib(V(topMovieIdx))
Variable containing:
1.00000e-02 *
2.3116
-1.7544
1.2235
⋮
4.6716
-1.8622
1.1731
[torch.cuda.FloatTensor of size 3000x1 (GPU 0)]
movie_ratings = [(b[0], movie_names[i]) for i,b in zip(topMovies,movie_bias)]
What are the worst movies?
sorted(movie_ratings, key=lambda o: o[0])[:15]
[(-0.049937896, 'Sin City (2005)'),
(-0.049869832, 'Winnie the Pooh and the Blustery Day (1968)'),
(-0.049756341, 'Bringing Down the House (2003)'),
(-0.049732186, 'Maltese Falcon, The (1941)'),
(-0.049730305, 'Fish Called Wanda, A (1988)'),
(-0.049677063, 'Nell (1994)'),
(-0.049676962, 'Spirited Away (Sen to Chihiro no kamikakushi) (2001)'),
(-0.049667355, 'Sunshine (2007)'),
(-0.049643833, 'Cider House Rules, The (1999)'),
(-0.049607702, '2001: A Space Odyssey (1968)'),
(-0.049597319, 'Penelope (2006)'),
(-0.049578078, 'Inconvenient Truth, An (2006)'),
(-0.049529426, 'Out of Sight (1998)'),
(-0.049520683, "Coal Miner's Daughter (1980)"),
(-0.049472842, 'Far from Heaven (2002)')]
sorted(movie_ratings, key=itemgetter(0))[:15]
[(-0.049937896, 'Sin City (2005)'),
(-0.049869832, 'Winnie the Pooh and the Blustery Day (1968)'),
(-0.049756341, 'Bringing Down the House (2003)'),
(-0.049732186, 'Maltese Falcon, The (1941)'),
(-0.049730305, 'Fish Called Wanda, A (1988)'),
(-0.049677063, 'Nell (1994)'),
(-0.049676962, 'Spirited Away (Sen to Chihiro no kamikakushi) (2001)'),
(-0.049667355, 'Sunshine (2007)'),
(-0.049643833, 'Cider House Rules, The (1999)'),
(-0.049607702, '2001: A Space Odyssey (1968)'),
(-0.049597319, 'Penelope (2006)'),
(-0.049578078, 'Inconvenient Truth, An (2006)'),
(-0.049529426, 'Out of Sight (1998)'),
(-0.049520683, "Coal Miner's Daughter (1980)"),
(-0.049472842, 'Far from Heaven (2002)')]
What’s the best movie?
sorted(movie_ratings, key=lambda o: o[0], reverse=True)[:15]
[(0.049996726, 'Basquiat (1996)'),
(0.04998317, 'Grindhouse (2007)'),
(0.04992019, 'Beneath the Planet of the Apes (1970)'),
(0.049862832, 'Get Shorty (1995)'),
(0.049845789, 'Night of the Living Dead (1968)'),
(0.049809847, 'Tomorrow Never Dies (1997)'),
(0.049781345, 'Glengarry Glen Ross (1992)'),
(0.049769394, 'Misérables, Les (1995)'),
(0.049750172, 'From Hell (2001)'),
(0.049735427, 'Catwoman (2004)'),
(0.049725704, 'Battleship Potemkin (1925)'),
(0.049607269, 'Bone Collector, The (1999)'),
(0.049606908, 'Perfume: The Story of a Murderer (2006)'),
(0.049585488, 'Frequency (2000)'),
(0.049541574, "Ender's Game (2013)")]
Embedding Interpretation
Let’s try and flatten this space so that we can interpret it better. Some techniques to think about are : PCA or SVD which are decomposition methods to reduce our dimensionality.
movie_emb = to_np(m.i(V(topMovieIdx)))
movie_emb.shape
(3000, 50)
We are reducing the 50 dimensionality to a 3-dimensional approximation
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
movie_pca = pca.fit(movie_emb.T).components_
movie_pca.shape
(3, 3000)
Lets look at the reduced dimensionality and interpret the meaning
fac0 = movie_pca[0]
movie_comp = [(f, movie_names[i]) for f,i in zip(fac0, topMovies)]
lets look at the 1st dimension: we call it easy watching vs. serious
sorted(movie_comp, key=itemgetter(0), reverse=True)[:10]
[(0.054308776, 'Bonfire of the Vanities (1990)'),
(0.052916676, 'Ex Machina (2015)'),
(0.052070759, 'Falling Down (1993)'),
(0.051866416, 'Nosferatu (Nosferatu, eine Symphonie des Grauens) (1922)'),
(0.050818264, 'Quantum of Solace (2008)'),
(0.050795961, 'Lilies of the Field (1963)'),
(0.049873799, 'Illusionist, The (2006)'),
(0.049717102, 'Ronin (1998)'),
(0.049355291, 'Bitter Moon (1992)'),
(0.048397031, 'Ella Enchanted (2004)')]
sorted(movie_comp, key=itemgetter(0))[:10]
[(-0.06548804, 'Hate (Haine, La) (1995)'),
(-0.054825306, 'Sandlot, The (1993)'),
(-0.053414859, 'Ruthless People (1986)'),
(-0.052211139, 'Simple Plan, A (1998)'),
(-0.051708255, 'Hairspray (1988)'),
(-0.049773846, 'Little Miss Sunshine (2006)'),
(-0.048778363, 'Black Beauty (1994)'),
(-0.048621822, 'Bonnie and Clyde (1967)'),
(-0.048216734, 'Kids (1995)'),
(-0.047948148, 'Tank Girl (1995)')]
let’s look at the 2nd dimension
fac1 = movie_pca[1]
movie_comp = [(f, movie_names[i]) for f,i in zip(fac1, topMovies)]
2nd dim best
sorted(movie_comp, key=itemgetter(0), reverse=True)[:10]
[(0.065224506, 'Kiss the Girls (1997)'),
(0.059658531, 'Fiddler on the Roof (1971)'),
(0.05408306, 'RoboCop (2014)'),
(0.053201783, 'Frenzy (1972)'),
(0.052245513, 'American Gangster (2007)'),
(0.050967816, 'Cutting Edge, The (1992)'),
(0.050565537, 'Reindeer Games (2000)'),
(0.05018561, 'Hearts of Darkness: A Filmmakers Apocalypse (1991)'),
(0.049161926, 'Badlands (1973)'),
(0.048389364, 'Mad Max: Fury Road (2015)')]
2nd dim worst
sorted(movie_comp, key=itemgetter(0))[:10]
[(-0.063395478, 'Pollyanna (1960)'),
(-0.06290257, "Monster's Ball (2001)"),
(-0.058774415, 'Mexican, The (2001)'),
(-0.058014624, 'Tin Men (1987)'),
(-0.056430273, 'Mad City (1997)'),
(-0.055390898, 'Men in Black II (a.k.a. MIIB) (a.k.a. MIB 2) (2002)'),
(-0.055204011, 'Identity (2003)'),
(-0.053047962, 'Fear (1996)'),
(-0.052593146, 'Underworld: Rise of the Lycans (2009)'),
(-0.050690483, 'Wedding Singer, The (1998)')]
idxs = np.random.choice(len(topMovies), 50, replace=False)
X = fac0[idxs]
Y = fac1[idxs]
plt.figure(figsize=(15,6))
plt.scatter(X, Y)
for i, x, y in zip(topMovies[idxs], X, Y):
plt.text(x,y,movie_names[i], color=np.random.rand(3)*0.7, fontsize=11)
plt.show()
Entity Embedding Layer
What if we replace all the words as features, we replace them with the embeddings instead. And then run GBM on top of it. This uses embedding of stores as a intermediate transformation and then run random forest or GBM on top of it. You can even use KNN on top of it and get a lot of improvement.
GBMs and RF train a lot faster than NN.
They also tried using embeddings:
- to plot the cities in Germany.
- to understand the closeness of stores vs. the embeddings of stores.
- on days of the week, or months.
Question on Skipgram to generate embeddings -> Discussion on Word2Vec
Started one sentence, and replaces 1 word with another cat. Then they made labels 1 if it was unchanged, and 0 if it was changed. And the model will try to find the fake sentences, but as a result, they have embeddings for other purposes. If you do this as matrix multiplier, (shallow),
- you can train this very quickly.
- can train on big dataset.
- embeddings that have really linear characteristics.
Ideally we need to move away from Word2Vec, its not very good at predictive power. The new state of the art is Language models with a deep RNN.
You either need labeled data, or you need to invent a task that will generate that
- ideally a task where the kinds of relationships are transferable to the ideal task
- in computer vision, lets recolor images, and have the NN guess if its been edited or not
- try and come up with more clever fake tasks.
-
Auto Encoder- force a large amount of variables down into a smaller layer, then back out again.
In computer vision, you can train on cats and dogs and use it for CT scans. Maybe it might work for language / NLP! (future research)
Aside on Rossman (from lesson 3)
- Talking about embedding
- Looking at Sunday effects
- Not looking at the Exploratory Data Analysis (EDA) for store closure.
-
MixedInputModelwas used
class MixedInputModel(nn.Module):
def __init__(self, emb_szs, n_cont, emb_drop, out_sz, szs, drops,
y_range=None, use_bn=False):
super().__init__()
self.embs = nn.ModuleList([nn.Embedding(c, s) for c,s in emb_szs])
for emb in self.embs: emb_init(emb)
n_emb = sum(e.embedding_dim for e in self.embs)
szs = [n_emb+n_cont] + szs
self.lins = nn.ModuleList([
nn.Linear(szs[i], szs[i+1]) for i in range(len(szs)-1)])
self.bns = nn.ModuleList([
nn.BatchNorm1d(sz) for sz in szs[1:]])
for o in self.lins: kaiming_normal(o.weight.data)
self.outp = nn.Linear(szs[-1], out_sz)
kaiming_normal(self.outp.weight.data)
self.emb_drop = nn.Dropout(emb_drop)
self.drops = nn.ModuleList([nn.Dropout(drop) for drop in drops])
self.bn = nn.BatchNorm1d(n_cont)
self.use_bn,self.y_range = use_bn,y_range
def forward(self, x_cat, x_cont):
x = [e(x_cat[:,i]) for i,e in enumerate(self.embs)]
x = torch.cat(x, 1)
x2 = self.bn(x_cont)
x = self.emb_drop(x)
x = torch.cat([x, x2], 1)
for l,d,b in zip(self.lins, self.drops, self.bns):
x = F.relu(l(x))
if self.use_bn: x = b(x)
x = d(x)
x = self.outp(x)
if self.y_range:
x = F.sigmoid(x)
x = x*(self.y_range[1] - self.y_range[0])
x = x+self.y_range[0]
return x
A Layer Deeper what does .fit() do?
Stochastic Gradient Descent (SGD)
Let’s work on solving a simple case of Ax + b. If we can do this we can apply the technique to other problems as well.
import torch
import sys
sys.path.append('../repos/fastai')
%matplotlib inline
from fastai.learner import *
from matplotlib import rcParams, animation, rc
from ipywidgets import interact, interactive, fixed
from ipywidgets.widgets import *
rc('animation', html='html5')
rcParams['figure.figsize'] = 3, 3
First let’s generate some fake data
# Here we generate some fake data
def lin(a,b,x): return a*x+b
def gen_fake_data(n, a, b):
x = s = np.random.uniform(0,1,n)
y = lin(a,b,x) + 0.1 * np.random.normal(0,3,n)
return x, y
x, y = gen_fake_data(50, 3., 8.)
A linear regression loss function
def mse(y_hat, y): return ((y_hat - y) ** 2).mean()
def mse_loss(a, b, x, y): return mse(lin(a,b,x), y)
Let’s test it out between 5 and 10.
mse_loss(10, 5, x, y)
4.3865950349551408
# generate some more data
x, y = gen_fake_data(10000, 3., 8.)
x.shape, y.shape
((10000,), (10000,))
#### label these as variables so that PyTorch will do the differentials
x,y = V(x),V(y)
Lets start initializing some weights.
# Create random weights a and b, and wrap them in Variables.
a = V(np.random.randn(1), requires_grad=True)
b = V(np.random.randn(1), requires_grad=True)
a,b
(Variable containing:
0.5666
[torch.FloatTensor of size 1], Variable containing:
1.1612
[torch.FloatTensor of size 1])
The gradient loop optim.sgd.step ...
-
.gradis where PyTorch calculates the differential - then we nudge the
aandbtensors in the direction of the gradient - you have to tell the gradients back to zero
-
zero_()the_means that the variable is changed in place
learning_rate = 1e-3
for t in range(10000):
# Forward pass: compute predicted y using operations on Variables
loss = mse_loss(a,b,x,y)
if t % 1000 == 0: print(loss.data[0])
# Computes the gradient of loss with respect to all Variables with requires_grad=True.
# After this call a.grad and b.grad will be Variables holding the gradient
# of the loss with respect to a and b respectively
loss.backward()
# Update a and b using gradient descent; a.data and b.data are Tensors,
# a.grad and b.grad are Variables and a.grad.data and b.grad.data are Tensors
a.data -= learning_rate * a.grad.data
b.data -= learning_rate * b.grad.data
# Zero the gradients
a.grad.data.zero_()
b.grad.data.zero_()
65.58589172363281
0.5537242889404297
0.1400136947631836
0.1267116665840149
0.1183580830693245
0.11194716393947601
0.10701844841241837
0.10322901606559753
0.100315622985363
0.0980757400393486
Can you do this with Numpy?
x, y = gen_fake_data(50, 3., 8.)
def rmse_loss(y,a,b,x): return np.sqrt(mse_loss(y,a,b,x))
a_guess,b_guess = -1., 1.
rmse_loss(y, a_guess, b_guess, x)
8.260525377243658
lr=0.01
def upd():
global a_guess, b_guess
y_pred = lin(a_guess, b_guess, x)
dydb = 2 * (y_pred - y)
dyda = x*dydb
a_guess -= lr*dyda.mean()
b_guess -= lr*dydb.mean()
Install ffmpeg
fig = plt.figure(dpi=100, figsize=(5, 4))
plt.scatter(x,y)
line, = plt.plot(x,lin(a_guess,b_guess,x))
plt.close()
def animate(i):
line.set_ydata(lin(a_guess,b_guess,x))
for i in range(30): upd()
return line,
ani = animation.FuncAnimation(fig, animate, np.arange(0, 20), interval=100)
ani
---------------------------------------------------------------------------
KeyError Traceback (most recent call last)
~/anaconda3/envs/fastai/lib/python3.6/site-packages/IPython/core/formatters.py in __call__(self, obj)
343 method = get_real_method(obj, self.print_method)
344 if method is not None:
--> 345 return method()
346 return None
347 else:
~/anaconda3/envs/fastai/lib/python3.6/site-packages/matplotlib/animation.py in _repr_html_(self)
1482 fmt = rcParams['animation.html']
1483 if fmt == 'html5':
-> 1484 return self.to_html5_video()
1485 elif fmt == 'jshtml':
1486 return self.to_jshtml()
~/anaconda3/envs/fastai/lib/python3.6/site-packages/matplotlib/animation.py in to_html5_video(self, embed_limit)
1407 # We create a writer manually so that we can get the
1408 # appropriate size for the tag
-> 1409 Writer = writers[rcParams['animation.writer']]
1410 writer = Writer(codec='h264',
1411 bitrate=rcParams['animation.bitrate'],
~/anaconda3/envs/fastai/lib/python3.6/site-packages/matplotlib/animation.py in __getitem__(self, name)
168 if not self.avail:
169 raise RuntimeError("No MovieWriters available!")
--> 170 return self.avail[name]
171
172 writers = MovieWriterRegistry()
KeyError: 'ffmpeg'
<matplotlib.animation.FuncAnimation at 0x7fca2a745cf8>
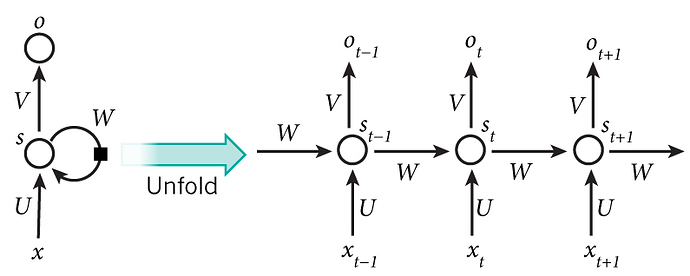
Recurrent Neural Network (RNN)!
%reload_ext autoreload
%autoreload 2
%matplotlib inline
from fastai.io import *
from fastai.conv_learner import *
from fastai.column_data import *
PATH='./'
get_data("https://s3.amazonaws.com/text-datasets/nietzsche.txt", f'{PATH}nietzsche.txt')
text = open(f'{PATH}nietzsche.txt').read()
print('corpus length:', len(text))
corpus length: 600893
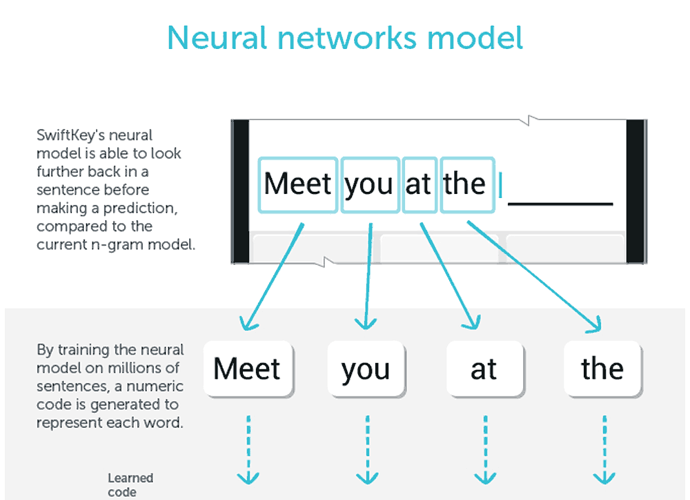
SwiftKey uses it
Super simple 1 hidden layer NN
Input : batchsize # inputs
Matrix product (linear)
Relu
Hidden layers () # activations batchsize x ct of hidden units
Matrix product (e.g. linear layer)
softmax
Output Activations # of classes
Super simple 1 hidden layer CNN
Input : batchsize # inputs
Convolution (stride 2)
Conv1 - filters
Flatten - Adaptive max pooling (average height and width
Fully connected layer
Matrix Product
Output classes # of classes
Super simple hidden layer model
- 2 hidden layer
- 3 matrix products
Input : char 1 vocab size # inputs
Fully connected layer 1
Fully connected layer 2 <--- character 2 input
Char3 output: vocab size
text[:400]
'PREFACE\n\n\nSUPPOSING that Truth is a woman--what then? Is there not ground\nfor suspecting that all philosophers, in so far as they have been\ndogmatists, have failed to understand women--that the terrible\nseriousness and clumsy importunity with which they have usually paid\ntheir addresses to Truth, have been unskilled and unseemly methods for\nwinning a woman? Certainly she has never allowed herself '
Let’s look at all the unique letters.
chars = sorted(list(set(text)))
vocab_size = len(chars)+1
print('total chars:', vocab_size)
total chars: 85
chars.insert(0, "\0")
''.join(chars[1:-6])
'\n !"\'(),-.0123456789:;=?ABCDEFGHIJKLMNOPQRSTUVWXYZ[]_abcdefghijklmnopqrstuvwxy'
Let’s make a lookup for chars to int.
char_indices = dict((c, i) for i, c in enumerate(chars))
indices_char = dict((i, c) for i, c in enumerate(chars))
idx = [char_indices[c] for c in text]
Each of these integers represent a character.
idx[:10]
[40, 42, 29, 30, 25, 27, 29, 1, 1, 1]
''.join(indices_char[i] for i in idx[:70])
'PREFACE\n\n\nSUPPOSING that Truth is a woman--what then? Is there not gro'
Three Character Model
Create inputs / targets
GOAL: Create a list of every 4th character, starting at the 0th, 1st, 2nd, then 3rd characters.
Create some datasets.
cs=3
c1_dat = [idx[i] for i in range(0, len(idx)-1-cs, cs)]
c2_dat = [idx[i+1] for i in range(0, len(idx)-1-cs, cs)]
c3_dat = [idx[i+2] for i in range(0, len(idx)-1-cs, cs)]
c4_dat = [idx[i+3] for i in range(0, len(idx)-1-cs, cs)]
Here are the 0, 1, 2 characters.
x1 = np.stack(c1_dat[:-2])
x2 = np.stack(c2_dat[:-2])
x3 = np.stack(c3_dat[:-2])
And our target variable, the 4th letter.
y = np.stack(c4_dat[:-2])
x1[:4], x2[:4], x3[:4]
(array([40, 30, 29, 1]), array([42, 25, 1, 43]), array([29, 27, 1, 45]))
y[:4]
array([30, 29, 1, 40])
x1.shape, y.shape
((200295,), (200295,))
Create the Simple Char Model
Input : char 1 input # inputs
Fully connected layer 1
Fully connected layer 2 <--- character 2 input
Fully connected layer 3 <--- character 3 input
output: Char4 output
Set hidden layer size and the number of factors for the embedding matrix.
n_hidden = 256
n_fac = 42
class Char3Model(nn.Module):
def __init__(self, vocab_size, n_fac):
super().__init__()
## embedding
self.e = nn.Embedding(vocab_size, n_fac)
# The 'green arrow' from our diagram - the layer operation from input to hidden
self.l_in = nn.Linear(n_fac, n_hidden)
# The 'orange arrow' from our diagram - the layer operation from hidden to hidden
self.l_hidden = nn.Linear(n_hidden, n_hidden)
# The 'blue arrow' from our diagram - the layer operation from hidden to output
self.l_out = nn.Linear(n_hidden, vocab_size)
def forward(self, c1, c2, c3):
in1 = F.relu(self.l_in(self.e(c1)))
in2 = F.relu(self.l_in(self.e(c2)))
in3 = F.relu(self.l_in(self.e(c3)))
h = V(torch.zeros(in1.size()).cuda())
h = F.tanh(self.l_hidden(h+in1))
h = F.tanh(self.l_hidden(h+in2))
h = F.tanh(self.l_hidden(h+in3))
return F.log_softmax(self.l_out(h))
in1 = F.relu(self.l_in(self.e(c1)))
Stick it through a linear layer, then a ReLU.
h = F.tanh(self.l_hidden(h+in1))
md = ColumnarModelData.from_arrays('.', [-1], np.stack([x1,x2,x3], axis=1), y, bs=512)
Create our PyTorch model (above)
m = Char3Model(vocab_size, n_fac).cuda()
it = iter(md.trn_dl)
*xs,yt = next(it)
t = m(*V(xs))
t
Variable containing:
-4.5326 -4.4424 -4.5330 ... -4.2526 -4.8234 -4.1015
-4.5132 -4.3008 -4.5556 ... -4.3550 -4.5121 -4.5760
-4.6016 -4.4866 -4.4367 ... -4.3994 -4.4466 -4.3081
... ⋱ ...
-4.4800 -4.3987 -4.3505 ... -4.2764 -4.6547 -4.7373
-4.5363 -4.4387 -4.5929 ... -4.0393 -4.3796 -4.3961
-4.3588 -4.4949 -4.3115 ... -4.1984 -4.5441 -4.6890
[torch.cuda.FloatTensor of size 512x85 (GPU 0)]
opt = optim.Adam(m.parameters(), 1e-2)
fit(m, md, 1, opt, F.nll_loss)
[ 0. 2.09804 5.12998]
set_lrs(opt, 0.001)
fit(m, md, 1, opt, F.nll_loss)
[ 0. 1.85502 4.3849 ]
Let’s test the model
def get_next(inp):
idxs = T(np.array([char_indices[c] for c in inp]))
p = m(*VV(idxs))
i = np.argmax(to_np(p))
return chars[i]
get_next('y. ')
'T'
get_next('ppl')
'e'
get_next(' th')
'e'
get_next('and')
' '
Let’s create an RNN
Input : char 1 input # inputs
Fully connected layer 1
Fully connected layer 2 RECURSE <--- character n input depending on the loop
output: Char4 output
Create input
cs=8
For each of 0 through 7, create a list of every 8th character with that starting point. These will be the 8 inputs to out model.
c_in_dat = [[idx[i+j] for i in range(cs)] for j in range(len(idx)-cs-1)]
Then create a list of the next character in each of these series. This will be the labels for our model.
c_out_dat = [idx[j+cs] for j in range(len(idx)-cs-1)]
xs = np.stack(c_in_dat, axis=0)
xs.shape
(600884, 8)
y = np.stack(c_out_dat)
So each column below is one series of 8 characters from the text.
xs[:cs,:cs]
array([[40, 42, 29, 30, 25, 27, 29, 1],
[42, 29, 30, 25, 27, 29, 1, 1],
[29, 30, 25, 27, 29, 1, 1, 1],
[30, 25, 27, 29, 1, 1, 1, 43],
[25, 27, 29, 1, 1, 1, 43, 45],
[27, 29, 1, 1, 1, 43, 45, 40],
[29, 1, 1, 1, 43, 45, 40, 40],
[ 1, 1, 1, 43, 45, 40, 40, 39]])
…and this is the next character after each sequence.
y[:cs]
array([ 1, 1, 43, 45, 40, 40, 39, 43])
val_idx = get_cv_idxs(len(idx)-cs-1)
md = ColumnarModelData.from_arrays('.', val_idx, xs, y, bs=512)
Note that we have a 8 layer network, due to the loop
class CharLoopModel(nn.Module):
def __init__(self, vocab_size, n_fac):
super().__init__()
self.e = nn.Embedding(vocab_size, n_fac)
self.l_in = nn.Linear(n_fac, n_hidden)
self.l_hidden = nn.Linear(n_hidden, n_hidden)
self.l_out = nn.Linear(n_hidden, vocab_size)
def forward(self, *cs):
bs = cs[0].size(0)
h = V(torch.zeros(bs, n_hidden).cuda())
#============= Our new loop ==============
for c in cs:
inp = F.relu(self.l_in(self.e(c)))
h = F.tanh(self.l_hidden(h+inp))
#============= Our new loop ==============
return F.log_softmax(self.l_out(h))
m = CharLoopModel(vocab_size, n_fac).cuda()
opt = optim.Adam(m.parameters(), 1e-2)
fit(m, md, 1, opt, F.nll_loss)
[ 0. 2.07544 2.0632 ]
set_lrs(opt, 0.001)
fit(m, md, 1, opt, F.nll_loss)
[ 0. 1.77987 1.79123]
Adding two things together is a bit dangerous, now we will modify layer to concat instead of add
This way we will not lose information.
class CharLoopConcatModel(nn.Module):
def __init__(self, vocab_size, n_fac):
super().__init__()
self.e = nn.Embedding(vocab_size, n_fac)
self.l_in = nn.Linear(n_fac+n_hidden, n_hidden)
self.l_hidden = nn.Linear(n_hidden, n_hidden)
self.l_out = nn.Linear(n_hidden, vocab_size)
def forward(self, *cs):
bs = cs[0].size(0)
h = V(torch.zeros(bs, n_hidden).cuda())
for c in cs:
#============ replace =============
inp = torch.cat((h, self.e(c)), 1)
#============ replace =============
inp = F.relu(self.l_in(inp))
h = F.tanh(self.l_hidden(inp))
return F.log_softmax(self.l_out(h))
m = CharLoopConcatModel(vocab_size, n_fac).cuda()
opt = optim.Adam(m.parameters(), 1e-3)
it = iter(md.trn_dl)
*xs,yt = next(it)
t = m(*V(xs))
fit(m, md, 1, opt, F.nll_loss)
[ 0. 1.80183 1.78611]
set_lrs(opt, 1e-4)
fit(m, md, 1, opt, F.nll_loss)
[ 0. 1.68999 1.69335]
Test our RNN
def get_next(inp):
idxs = T(np.array([char_indices[c] for c in inp]))
p = m(*VV(idxs))
i = np.argmax(to_np(p))
return chars[i]
get_next('for thos')
'e'
get_next('part of ')
't'
get_next('queens a')
'n'
RNN in PyTorch will make the layers for us
note that:
outp,h = self.rnn(inp, h) will give back a growing matrix (all hidden states)
quick comment
h = V(torch.zeros(1, bs, n_hidden)) we can actually have two directions (forward and backwards), or we can also do a multilayer RNN
class CharRnn(nn.Module):
def __init__(self, vocab_size, n_fac):
super().__init__()
self.e = nn.Embedding(vocab_size, n_fac)
# ===== torch! =================
self.rnn = nn.RNN(n_fac, n_hidden)
# ===== torch! =================
self.l_out = nn.Linear(n_hidden, vocab_size)
def forward(self, *cs):
bs = cs[0].size(0)
h = V(torch.zeros(1, bs, n_hidden))
inp = self.e(torch.stack(cs))
# ===== torch! =================
outp,h = self.rnn(inp, h)
# ===== torch! =================
return F.log_softmax(self.l_out(outp[-1]))
m = CharRnn(vocab_size, n_fac).cuda()
opt = optim.Adam(m.parameters(), 1e-3)
it = iter(md.trn_dl)
*xs,yt = next(it)
t = m.e(V(torch.stack(xs)))
t.size()
torch.Size([8, 512, 42])
Examine that last hidden state
ht = V(torch.zeros(1, 512,n_hidden))
outp, hn = m.rnn(t, ht)
outp.size(), hn.size()
(torch.Size([8, 512, 256]), torch.Size([1, 512, 256]))
t = m(*V(xs)); t.size()
torch.Size([512, 85])
fit(m, md, 4, opt, F.nll_loss)
[ 0. 1.8626 1.85105]
[ 1. 1.67591 1.66735]
[ 2. 1.60083 1.59047]
[ 3. 1.52933 1.5452 ]
Test the model
def get_next(inp):
idxs = T(np.array([char_indices[c] for c in inp]))
p = m(*VV(idxs))
i = np.argmax(to_np(p))
return chars[i]
get_next('for thos')
'e'
def get_next_n(inp, n):
res = inp
for i in range(n):
c = get_next(inp)
res += c
inp = inp[1:]+c
return res
Predict more than 1 character!
get_next_n('for thos', 40)
'for those the same the same the same the same th'
Comment on efficiency
array([[40, 42, 29, 30, 25, 27, 29, 1],
[42, 29, 30, 25, 27, 29, 1, 1],
[29, 30, 25, 27, 29, 1, 1, 1],
[30, 25, 27, 29, 1, 1, 1, 43],
[25, 27, 29, 1, 1, 1, 43, 45],
[27, 29, 1, 1, 1, 43, 45, 40],
[29, 1, 1, 1, 43, 45, 40, 40],
[ 1, 1, 1, 43, 45, 40, 40, 39]])
There’s a lot of similarity between the different rows. So lets rearrange.
array([[40, 42, 29, 30, 25, 27, 29, 1],
[ 1, 1, 43, 45, 40, 40, 39, 43],
[33, 38, 31, 2, 73, 61, 54, 73],
[ 2, 44, 71, 74, 73, 61, 2, 62],
[72, 2, 54, 2, 76, 68, 66, 54],
[67, 9, 9, 76, 61, 54, 73, 2],
[73, 61, 58, 67, 24, 2, 33, 72],
[ 2, 73, 61, 58, 71, 58, 2, 67]])
array([[42, 29, 30, 25, 27, 29, 1, 1],
[ 1, 43, 45, 40, 40, 39, 43, 33],
[38, 31, 2, 73, 61, 54, 73, 2],
[44, 71, 74, 73, 61, 2, 62, 72],
[ 2, 54, 2, 76, 68, 66, 54, 67],
[ 9, 9, 76, 61, 54, 73, 2, 73],
[61, 58, 67, 24, 2, 33, 72, 2],
[73, 61, 58, 71, 58, 2, 67, 68]])
Multioutput
Input : char 1 input # inputs
Fully connected layer 1
# --------------------------- RECURSE
Fully connected layer 2 <--- character n input depending on the loop
output: Char4 output
# ---------------------------
We want non-overlappy character sets.
c_in_dat = [[idx[i+j] for i in range(cs)] for j in range(0, len(idx)-cs-1, cs)]
Same thing but offset by 1 as our labels.
c_out_dat = [[idx[i+j] for i in range(cs)] for j in range(1, len(idx)-cs, cs)]
xs = np.stack(c_in_dat)
xs.shape
(75111, 8)
ys = np.stack(c_out_dat)
ys.shape
(75111, 8)
val_idx = get_cv_idxs(len(xs)-cs-1)
md = ColumnarModelData.from_arrays('.', val_idx, xs, ys, bs=512)
class CharSeqRnn(nn.Module):
def __init__(self, vocab_size, n_fac):
super().__init__()
self.e = nn.Embedding(vocab_size, n_fac)
self.rnn = nn.RNN(n_fac, n_hidden)
self.l_out = nn.Linear(n_hidden, vocab_size)
def forward(self, *cs):
bs = cs[0].size(0)
h = V(torch.zeros(1, bs, n_hidden))
inp = self.e(torch.stack(cs))
outp,h = self.rnn(inp, h)
return F.log_softmax(self.l_out(outp))
m = CharSeqRnn(vocab_size, n_fac).cuda()
opt = optim.Adam(m.parameters(), 1e-3)
it = iter(md.trn_dl)
*xst,yt = next(it)
Let’s make a custom loss function
return F.nll_loss(inp.view(-1,nh), targ) flatten inputs and targets.
- PyTorch: The first axis is the sequence length (time steps)
- PyTorch: The second axis is the batch size
- PyTorch: The third axis is the size of the hidden layer itself
.contiguous() - to get rid of a warning because of transpose errors
def nll_loss_seq(inp, targ):
sl,bs,nh = inp.size()
targ = targ.transpose(0,1).contiguous().view(-1)
return F.nll_loss(inp.view(-1,nh), targ)
fit(m, md, 4, opt, nll_loss_seq)
[ 0. 1.10973 0.94373]
[ 1. 0.83671 0.76858]
[ 2. 0.71814 0.68435]
[ 3. 0.64689 0.63013]
set_lrs(opt, 1e-4)
fit (model, model data generator, optimizer, loss function)
fit(m, md, 1, opt, nll_loss_seq)
[ 0. 0.60356 0.61313]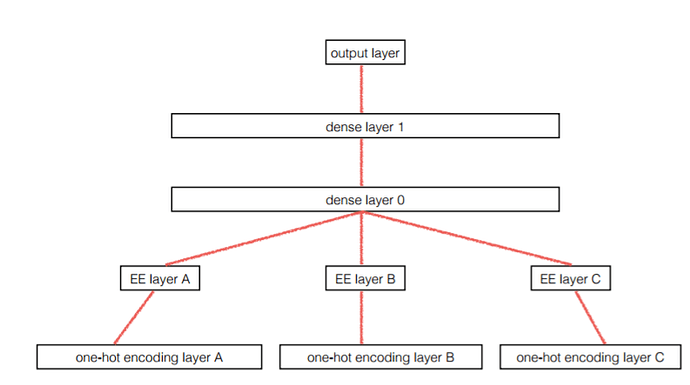


 )
)