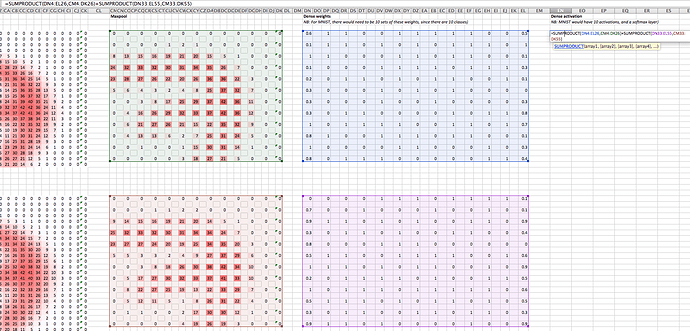
I was looking over this xls spreadsheet a bit more in detail.
I was interested in reviewing exactly what operation filters apply to an image in a convolutional layer.
OBSERVATION: in the beginning of the notebook, Jeremy uses a handwritten formula demonstrate the application of the filter, as such:
Later, he uses SUMPRODUCT, as such:
QUESTION: Are these the same operation?
ANSWER: Yes. If you do the math by hand you will see that the same thing is happening and the two methods will result in the same outcome. Why he chose to do it both ways, I’m not sure.
FOLLOW UP QUESTION: So what is the actual name for this operation?
ANSWER: The operation being performed here actually a Frobenius inner product. From what I can tell, this is a somewhat unusual operation in linear algebra. I looked in my undergraduate linear algebra book, and it wasn’t even in it.
On the slack channel, it was referred to being called a ‘convolution’.
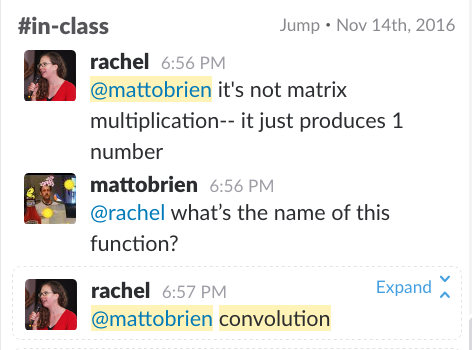
It seems like a good name but I’m not sure if it’s the most accurate name, from a mathematical perspective? Would love someone else to chime in here as set me straight if need be.
@brendan: Could I be so bold as to suggest maybe you throw in a bit about the Frobenius inner product on the linear algebra cheat sheet? It might be good to get into the habit (speaking collectively) to begin throwing this name around more frequently, considering this is how filters appear to operate. It is very similar to the Hadamard product that you discuss on the cheat sheet, but still different.