Complex numbers

Array programming
1

Here are some nice introductions to complex numbers:

And then beyond complex…

And just for fun…

2 Likes
2

I wrote a quick primer here:

3

(edit, pre-note: later when you see ∠- and ∠+, imagine them overprinted,)

As a consequence of needing phasors for electrical engineering, I’ve been reasonably comfortable with complex numbers, but now I realise this was more from just accepting (many years ago in undergrad) the “abstract notion” of its “imaginary” form works in the formulas.

Having now refreshed my knowledge with these videos, I’ve come to the conclusion that the way complex numbers are first-taught using catesian coordinates as “a magnitude in one dimension and second magnitude in another dimension” is wrong! It risks the confusing query “What’s the meaning of this second magnitude, and the meaning of this second dimension?” for which many don’t have a good intuitive answer for a child.

So I was considering this APL example of DIRECTION…
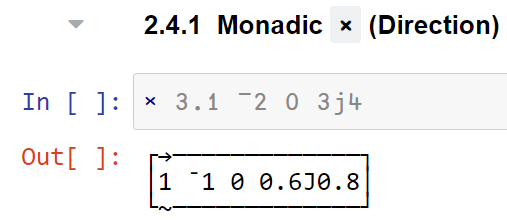
image

and thinking that 53° would be a better conceptual “direction” than 0.6J0.8.
i.e. DIRECTION is better conceptualised as [ 1∠0 1∠180 0 1∠53 ]

And then I was considering where the quaternions video says… “William Rowan Hamilton spent much of his life seeking a three dimensional number system, but… what he needed was not to add a single dimension to the complex numbers, but to add two more imaginary dimensions”

Two rotated lines can only have one angle between them, but that creates a plane that two degrees of freedom to rotate, for two more angles. So a total of three angles and a scalar.

Which lead to the insight that its all about ROTATION. Rotation conceptually unifies and simplifies everything. I think this even impacts all the way back to one of the most basic things taught to children:

-1 times -1 equals 1

because when the child considers this and asks “Why?” the only answer I had before was “Because!”, thats really a poor answer, and this proof doesn’t help.

So whats an alternative?

Consider a child that has only learnt to count positive numbers and addition, but not yet subtraction or negative numbers. Stand them on a number line drawn on the ground - they are a robot that can only move forward. So they can add 3 apples and 5 apples by walking forward. Now to take away 2 apples, requires them (the robot) to “turn around”, so lets write that 2∠̵, because they’ve turned all the way around on the line, and its not harder much harder than writing -2. And then original natural numbers with no turn we’ll label ∠ .

So rather than teaching subtraction like this… 3 + 5 - 2 and “counting backwards”,
we first teach “directional-addition” like this 3∠ + 5∠ + 2∠̵. Subtraction not required.

So that sets up a framework for kids to be curious about “What happens if I only turn part way?” and then they can be taught angles and the teacher says “see this special half turn direction, lets call it ∠+, because it makes a cross with the original line”

So then 5 + 3i becomes 5 + 3∠+ and taught in primary school. Students can roleplay walking 5∠-36 then 3∠+ then 4∠̵ in the yard to get back to where they started, or do the same with Logo turtle programs.

1 Like
4

For Advent of Code fans, complex numbers in APL is a convenient way to deal with grids, points etc, too. My crib sheet:

0j1⊥¨    0j1⊥   ⍝ pair(s) of reals -> complex
11 9∘○¨  11 9○  ⍝ complex -> pair(s) of reals
|z0-z1          ⍝ distance between two points
0j1×z   0j¯1×z  ⍝ rotate by ±90° around (0,0)
0j1*⍳4          ⍝ the four cardinal directions
+z       -+z    ⍝ reflect across x or y axis
+\0,z           ⍝ sequence of steps -> path
¯2-/z           ⍝ path -> sequence of steps
0j1⊥¨n-⍳2⍴1+2×n ⍝ lattice centred on (0,0)
1 Like