I am trying to work on building an variational autoencoder in Keras, with an input shape of X= (1,32) and Y= (1,16).
I made 2 models, one for the prediction of Y, and the second for reconstruction. The reconstruction train very well, however, the predictor cant predict the Y correctly. I am working in biology field, I want to predict the binary vector of Y through X.
I will explain mode: X is a binary vector of length n (e.g., X(1,:) = [0/1, 0/1, ..., 0/1]).
Y is a binary vector of length m, where m < n (e.g., Y(1,:) = [0/1, 0/1, ..., 0/1]).
For each X => Y
the data is like that : for example a sample :
X = [1,0,1,1,1,0,1,0,1,0,1,1,0,1] and its Y=[0,1,1,1,1,0,1]
My objective is to develop a machine learning model M that can predict the vector Y from the vector X with an accuracy greater than 95%. I accept only an error of 1 bit ! not more.
This is an example of the dataset, you can download it from link.
This is my model:
from keras.layers import Lambda, Input, Dense, Reshape, RepeatVector, Dropout
from keras.models import Model
from keras.datasets import mnist
from keras.losses import mse, binary_crossentropy
from keras.utils import plot_model
from keras import backend as K
from keras.constraints import unit_norm, max_norm
import tensorflow as tf
from scipy import stats
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import argparse
import os
from sklearn.manifold import MDS
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import mean_squared_error, r2_score
from keras.layers import Input, Dense, Flatten, Lambda,Conv1D, BatchNormalization, MaxPooling1D, Activation
from keras.models import Model
import keras.backend as K
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
def sampling(args):
"""Reparameterization trick by sampling fr an isotropic unit Gaussian.
# Arguments:
args (tensor): mean and log of variance of Q(z|X)
# Returns:
z (tensor): sampled latent vector
"""
z_mean, z_log_var = args
batch = K.shape(z_mean)[0]
dim = K.int_shape(z_mean)[1]
# by default, random_normal has mean=0 and std=1.0
epsilon = K.random_normal(shape=(batch, dim))
thre = K.random_uniform(shape=(batch,1))
return z_mean + K.exp(0.5 * z_log_var) * epsilon
# Load my Data
training_feature = X
ground_truth_r = Y
np.random.seed(seed=0)
original_dim = 32
# Define VAE model components
input_shape_x = (32, )
input_shape_r = (16, )
intermediate_dim = 32
latent_dim = 32
# Encoder network
inputs_x = Input(shape=input_shape_x, name='encoder_input')
inputs_x_dropout = Dropout(0.25)(inputs_x)
inter_x1 = Dense(128, activation='tanh')(inputs_x_dropout)
inter_x2 = Dense(intermediate_dim, activation='tanh')(inter_x1)
z_mean = Dense(latent_dim, name='z_mean')(inter_x2)
z_log_var = Dense(latent_dim, name='z_log_var')(inter_x2)
z = Lambda(sampling, output_shape=(latent_dim,), name='z')([z_mean, z_log_var])
encoder = Model(inputs_x, [z_mean, z_log_var, z], name='encoder')
# Decoder network for reconstruction
latent_inputs = Input(shape=(latent_dim,), name='z_sampling')
inter_y1 = Dense(intermediate_dim, activation='tanh')(latent_inputs)
inter_y2 = Dense(128, activation='tanh')(inter_y1)
outputs_reconstruction = Dense(original_dim)(inter_y2)
decoder = Model(latent_inputs, outputs_reconstruction, name='decoder')
# Separate network for prediction from latent space
outputs_prediction = Dense(Y.shape[1])(inter_y2) # Adjust Y.shape[1] as per your data
predictor = Model(latent_inputs, outputs_prediction, name='predictor')
from tensorflow.keras.metrics import AUC
# Instantiate VAE model with two outputs
outputs_vae = [decoder(encoder(inputs_x)[2]), predictor(encoder(inputs_x)[2])]
vae = Model(inputs_x, outputs_vae, name='vae_mlp')
vae.compile(optimizer='adam', loss=['mean_squared_error', 'mean_squared_error'], metrics=[AUC()])
# Train the model
history = vae.fit(X, [X, Y], epochs=200, batch_size=16, shuffle=True,validation_data=(XX,[XX, YY]), validation_split=0.05)
# Save models and plot training/validation loss
encoder.save("BrmEnco Third.h5")
decoder.save("BrmDeco Third.h5")
predictor.save("BrmPred Third.h5")
vae.save("BrmAuto Third.h5")
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(history.history['decoder_loss'], label='Decoder Training Loss')
plt.plot(history.history['val_decoder_loss'], label='Decoder Validation Loss')
plt.title('Decoder Loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(history.history['predictor_loss'], label='Predictor Training Loss')
plt.plot(history.history['val_predictor_loss'], label='Predictor Validation Loss')
plt.title('Predictor Loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend()
plt.show()
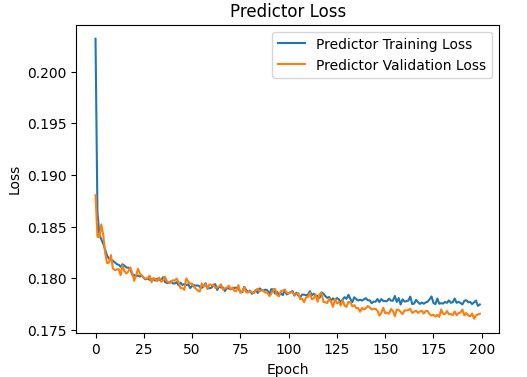
This is the plot of the predictor :
The model always gives always bad predictions with MAE=0.28. I use the following code to test:
import numpy as np
from sklearn.metrics import mean_absolute_error
from keras.models import load_model
import numpy as np
#encoder = load_model("Enco.h5", compile=False)
#decoder = load_model("Deco.h5", compile=False)
#predictor = load_model("Pre.h5", compile=False)
#vae = load_model("Aut.h5", compile=False)
###################################################
N =22
Challenge =TEST[N, :32].reshape(1, -1);
X_new = Challenge # Replace with your new data
# Encode X_new to get the latent space representation
a,v,z = encoder.predict(X_new)
# Use the predictor to predict Y from the latent representation
# Y_pred is the predicted output
print(TEST[N,32:].reshape(1, -1)*-1.)
print(predictor.predict(z).round()*-1)
Challenge =TEST[:, :32]
_, _, z = encoder.predict(Challenge)
Y_pred = predictor.predict(z)
MAE= mean_absolute_error(TEST[:, 32:], Y_pred.round())
print( "The MAE: ", MAE)