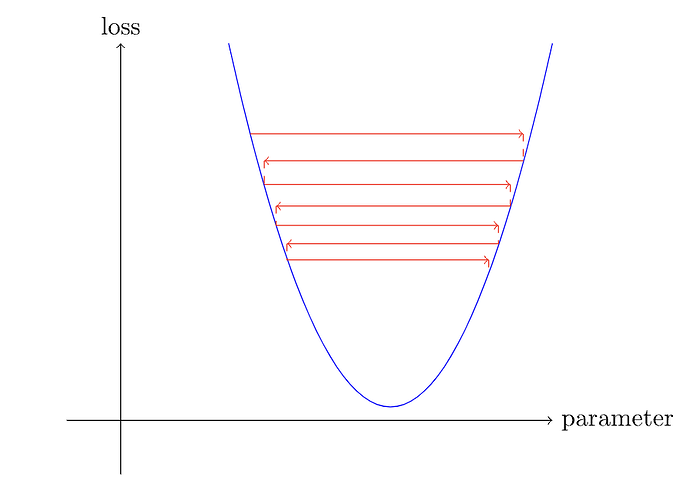
From the image above (taken from figure 4-4 in chapter 4 of the book), while it looks like the loss is bouncing around, it does appear to be slowly moving down towards the global optimum.
Is this true? Will/could a bouncy high learning rate eventually converge to the global optimum? Or, as the image above it (figure 4-3) in the chapter illustrates, is there a chance a high learning rate means it may never converge and it could miss the global optimum entirely by overshooting the minimum?
In other words, does it just depend on a case by case basis?
Here are ChatGPT’s (GPT 4 Turbo’s) thoughts (but it would be useful to verify by a real person!):
- Yes, a high learning rate can overshoot the global minimum
- There is a chance that a high learning rate may converge onto the global minimum, but this depends on luck and is unreliable
The loss surface given above is a parabola and the iterations will converge, but in real life such a simple surface is not very common. They generally contains a large number steep valleys and uneven shapes, wherein the comments provided by ChatGPT are indeed applicable.
1 Like
In the case in the picture, you have only one min. Generally, you can use or build scheduler with sin and cos functions, giving the rhythm to the SGD. When LR is going to reach declared max then momentum is going to declare min. In other words SGD don’t move too much (lower momentum), because updating weights will be high (higher learning rate). If you want to go deeper in this topic, I suggest you to look at Pytorch documentation, which strongly is aligned to fast.ai, catch the url:
https://pytorch.org/docs/stable/generated/torch.optim.lr_scheduler.OneCycleLR.html