Not sure about this new learn.recorder.plot() feature showing things like:
Min numerical gradient: 6.31E-07
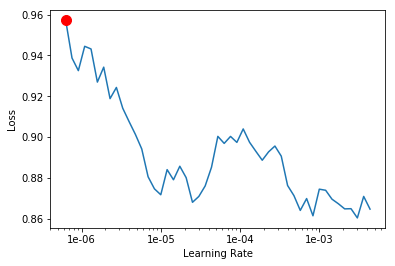
It works great on a well-behaved graph, but at times this is then not very useful, or plain misleading if someone were to use that data?
Perhaps it needs a sanity check and not display things that while mathematically correct are not useful at all?