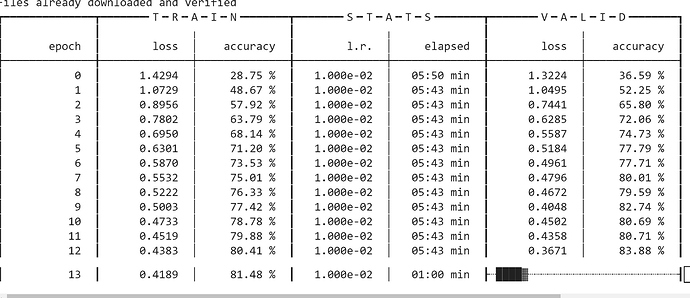
I have a working version for fastai2 now, but my code is still a bit rough around the edges I feel, performance isn’t quite on par with AdamW yet, but sharing here for a start. I’ve only been testing it with machine translation with a Transformer model so can’t guarantee this code will work without a few tweaks for vision, I think it should tho
It is a bit of a pig when it comes to memory usage, I can only fit a 57M parameter Transformer (2 enc/2 dec) on my 2080 (without MixedPrecision for now) whereas before a 89M model (6/6) worked fine, but mixed precision will help with that and I’m hoping the improvement in performance will make up for it.
Note this implementation doesn’t work with MixedPrecision yet, I think there is something going on with scaling the gradients I need to figure out, will hopefully get it figured out soon.
Weights and Biases experiment runs are here
Callback + Optimizer + Learner patch
Right now the optimizer looks more or less the same as AdamW, however I needed to add a callback to calculate the diagonal of the hessian as I couldn’t do it from within the optimizer functions (happy to hear if someone manages to figure this out tho!). The optimizer code is more or less the same as Adam, the callback is where the magic happens.
Shoutout to @LessW2020 for his code, helped a lot in getting this working
Optimizer
average_sqr_diag_hessian - almost identical to average_sqr_grad
def average_sqr_diag_hessian(p, sqr_mom, dampening=True, sqr_avg_diag_hessian=None, hutchinson_trace=None, **kwargs):
if sqr_avg_diag_hessian is None: sqr_avg_diag_hessian = torch.zeros_like(p.grad.data)
damp = 1-sqr_mom if dampening else 1.
sqr_avg_diag_hessian.mul_(sqr_mom).addcmul_(hutchinson_trace, hutchinson_trace, value=damp)
return {'sqr_avg_diag_hessian': sqr_avg_diag_hessian}
adahessian_step - similar to adam_step
def adahessian_step(p, lr, mom, step, sqr_mom, grad_avg, sqr_avg_diag_hessian, hessian_power, eps, **kwargs):
"Step for Adam with `lr` on `p`"
debias1 = debias(mom, 1-mom, step)
debias2 = debias(sqr_mom, 1-sqr_mom, step)
p.data.addcdiv_(grad_avg, ((sqr_avg_diag_hessian/debias2).sqrt() ** hessian_power) + eps, value = -lr / debias1)
return p
AdaHessian - tying it all together (DONT USE ME FOR NOW)
#@log_args(to_return=True, but_as=Optimizer.__init__)
#def AdaHessian(params, lr=0.1, hessian_power=1, hutchinson_trace=None, mom=0.9, #sqr_mom=0.98, eps=1e-4, wd=0.0, decouple_wd=True):
# "A `Optimizer` for Adam with `lr`, `mom`, `sqr_mom`, `eps` and `params`"
# cbs = [weight_decay] if decouple_wd else [l2_reg]
# cbs += [partial(average_grad, dampening=True), average_sqr_diag_hessian, step_stat, adahessian_step]
# return Optimizer(params, cbs, lr=lr, mom=mom, sqr_mom=sqr_mom, hessian_power=hessian_power, eps=eps, wd=wd)
Callback
class HutchinsonTraceCallback(Callback):
run_before=MixedPrecision
def __init__(self, block_length=1):
self.block_length = block_length
def _clip_grad_norm(self, max_norm=0., params=None):
"""
From FairSeq opimizer - Clips gradient norm.
"""
if max_norm > 0:
return torch.nn.utils.clip_grad_norm_(params, max_norm)
else:
return math.sqrt(sum(p.grad.data.norm()**2 for p in params if p.grad is not None))
def after_backward(self):
"""
compute the Hessian vector product with a random vector v, at the current gradient point,
i.e., compute the gradient of <gradsH,v>.
:param gradsH: a list of torch variables
:return: a list of torch tensors
"""
device = self.learn.dls.device
params, grads = [], []
for p in self.learn.model.parameters():
if p.requires_grad and p.grad is not None:
params.append(p)
grads.append(p.grad)
grad_norm = self._clip_grad_norm(max_norm=0., params=params) # Not sure if this is needed...
zs = [torch.randint_like(p, high=2).to(device) * 2.0 - 1.0 for p in params]
h_zs = torch.autograd.grad(grads, params, grad_outputs=zs, only_inputs=True, retain_graph=False)
# @LESSW CODE
hutchinson_trace = []
for hz, z in zip(h_zs, zs):
param_size = hz.size()
if len(param_size) <= 2: # for 0/1/2D tensor
tmp_output = torch.abs(hz * z) + 0. #.float()
hutchinson_trace.append(tmp_output) # Hessian diagonal block size is 1 here.
elif len(param_size) == 4: # Conv kernel
tmp_output = torch.abs(torch.sum(torch.abs(hz * z) + 0., dim=[2, 3], keepdim=True)).float() / z[0, 1].numel() # Hessian diagonal block size is 9 here: torch.sum() reduces the dim 2/3.
hutchinson_trace.append(tmp_output)
# Add hutchinson_trace to optimizer state
for i, (_,_,state,_) in enumerate(self.learn.opt.all_params(with_grad=True)):
state['hutchinson_trace'] = hutchinson_trace[i]
def after_step(self): # Is this needed?
for h in hutchinson_trace:
h.zero_()
for i, (_,_,state,_) in enumerate(self.learn.opt.all_params(with_grad=True)):
state['hutchinson_trace'].zero_()
Learner Patch
@patch
def _backward(self:Learner): self.loss.backward(create_graph=True)
Just add the callback and optimizer to your Learner and you should be good to go!
 (or on the TODO). Also fantastic work, I figured you were on this
(or on the TODO). Also fantastic work, I figured you were on this 
 ) , might also be worth a PR after some more testing if its performance in practice can meet expectations
) , might also be worth a PR after some more testing if its performance in practice can meet expectations