Phase 1 Review
Sorry I was busy this weekend and didn’t get a chance to respond.
I am excited to see how others approached the problems. Thank you @Moody for compiling the problems.
Here is some commentary on my solutions.
1: Counting DNA Nucleotides
fn ← +/'ACGT'∘.=,
This was an eye-opening experience for me. Using the outer product to build a relationship table
dna ← 'AGCTTTTCATTCTGAC'
'ACGT' ∘.= dna
1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0
0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 1
0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0
0 0 0 1 1 1 1 0 0 1 1 0 1 0 0 0
and then summing
+/ 'ACGT' ∘.= dna
3 4 2 7
was a perfect example of “Thinking with Arrays”. The , was to catch an edge case.
2: Attack of the Mutations!
fn ← +/≠
This solution creates a boolean mask where the arrays are not equal and then sums. Pretty straightforward.
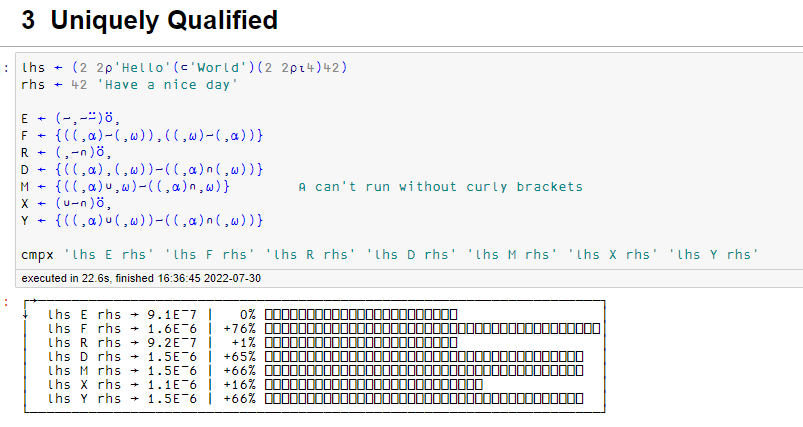
3: Uniquely Qualified
fn ← (~,~⍨)⍥,
From what I understood this question is asking for the “Exclusive Or” of the arguments.
The Without function A ~ B provided the elements of A without the elements of B. For the solution, I would need to reverse B ~ A as well. The Commute operator ⍨ flips the arguments. Finally, I join the lists together with ⍥,. I am not so comfortable with the use of the Over operator ⍥ but it worked!
4: In the Long One…
fn ← ⌈/0,≢¨⍤⊆⍨∘,
My approach here came from experimenting with applying the partition function to a binary array.
b ← 1 1 1 0 1 1 0 0 1 1 1 1 0
(⊆⍨) b
┌─────┬───┬───────┐
│1 1 1│1 1│1 1 1 1│
└─────┴───┴───────┘
Now I wanted to count each box
(≢¨⍤⊆⍨) b
3 2 4
and then take the maximum
(⌈/≢¨⍤⊆⍨) b
4
5: Stairway to Heaven (with apologies to Led Zeppelin)
fn ← ⌽∘↑⍴∘'⎕'¨∘⍳
My approach here was to generate a sequence of boxes from 1 to n, and then reshape it to look correct.
(⍴∘'⎕'¨∘⍳) 5
┌─┬──┬───┬────┬─────┐
│⎕│⎕⎕│⎕⎕⎕│⎕⎕⎕⎕│⎕⎕⎕⎕⎕│
└─┴──┴───┴────┴─────┘
Here ⍴∘'⎕' is applied to each number from iota ⍳. The last bit opens the boxed array and rotates it.
(⌽∘↑⍴∘'⎕'¨∘⍳) 5
⎕
⎕⎕
⎕⎕⎕
⎕⎕⎕⎕
⎕⎕⎕⎕⎕
6: Pyramid Scheme
fn←⌊∘⌽∘⊖⍨(∘.⌊⍨∘⍳0⌈¯1+×∘2)
My thought process here was to generate a matrix, flip it around and then take the minimum. The phrase 0⌈¯1+×∘2 came from the question and calculates the appropriate size for the matrix. Next up was to generate a matrix. I decided to use the outer product with a minimum ⌊ as the function to be applied.
(∘.⌊⍨∘⍳0⌈¯1+×∘2) 3
1 1 1 1 1
1 2 2 2 2
1 2 3 3 3
1 2 3 4 4
1 2 3 4 5
Then rotate it
⌽∘⊖(∘.⌊⍨∘⍳0⌈¯1+×∘2) 3
5 4 3 2 1
4 4 3 2 1
3 3 3 2 1
2 2 2 2 1
1 1 1 1 1
Finally, take the minimum of these two matrices
(⌊∘⌽∘⊖⍨(∘.⌊⍨∘⍳0⌈¯1+×∘2)) 3
1 1 1 1 1
1 2 2 2 1
1 2 3 2 1
1 2 2 2 1
1 1 1 1 1
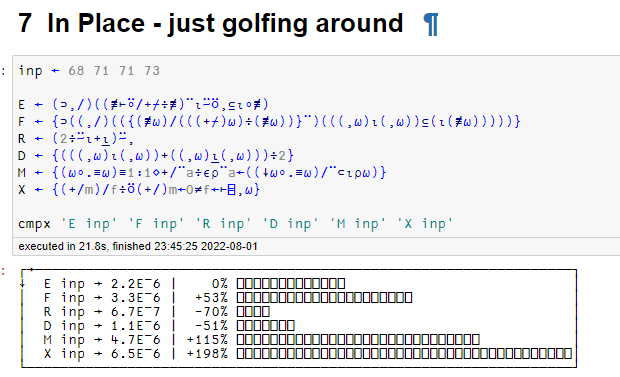
7: Just Golfing Around
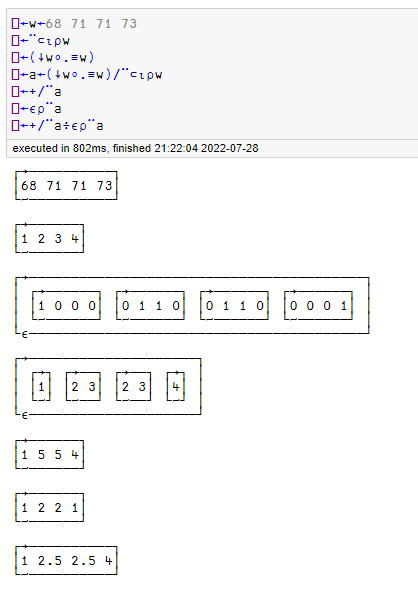
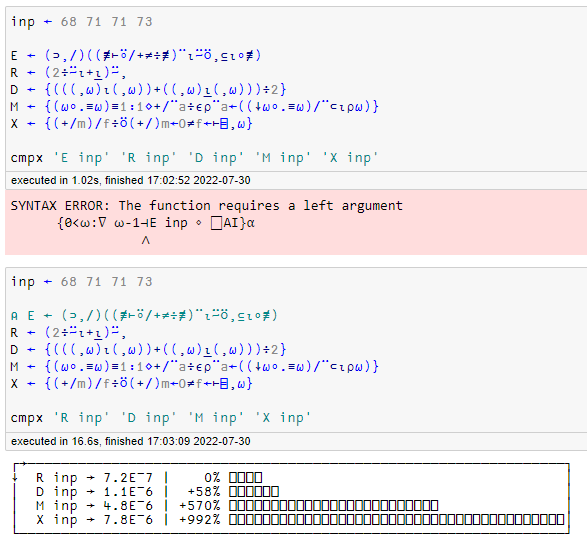
fn ← (⊃,/)((≢⊢⍤/+⌿÷≢)¨⍳⍨⍥,⊆⍳∘≢)
This problem caused me a lot of difficulties. My initial approach was to do a similar technique to problem 4 where I use the partition function.
t ← 68 71 71 73
⊆⍨ t
┌──┬─────┬──┐
│68│71 71│73│
└──┴─────┴──┘
but the issue here is I need to group the places not the value of the score. Luckily the function argument is always sorted so we can use iota ⍳ to generate a list of places
(⍳≢) t
1 2 3 4
and I will also use the dyadic for of iota which gives me the index of the first occurrence of each score
⍳⍨ t
1 2 2 4
These two functions are joined by a partition ⊆ to form the separate rankings
(⍳⍨⊆⍳∘≢) t
┌─┬───┬─┐
│1│2 3│4│
└─┴───┴─┘
Next, I wanted to find the average of each box.
((+⌿÷≢)¨⍳⍨⊆⍳∘≢) t
1 2.5 4
but the problem was I needed to replicate the average for tied places. The replicate function / was used along with ≢.
((≢⊢⍤/+⌿÷≢)¨⍳⍨⍥,⊆⍳∘≢) t
┌─┬───────┬─┐
│1│2.5 2.5│4│
└─┴───────┴─┘
It turns out the slash symbol is tricky because sometimes it can be a function and other times it can be an operator. In this case, I appended a right tack to the slash to force it to be a function rather than an operator.
All that is left is to concatenate the values and unbox the result
(⊃,/)((≢⊢⍤/+⌿÷≢)¨⍳⍨⍥,⊆⍳∘≢) t
1 2.5 2.5 4
8: Let’s Split!
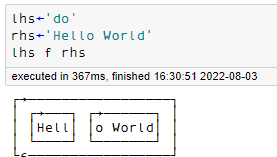
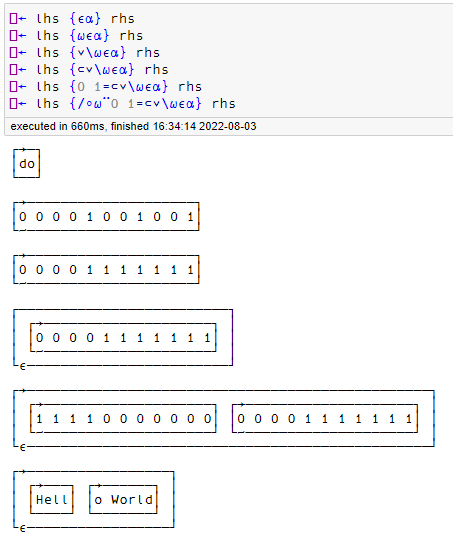
fn ← {n←⍺(-∘1(⌊/⊣⍳⍨(⍬∘,⊢)))⍵⋄(n↑⍵)(n↓⍵)}
For this problem, we were asked to split a list based on the first occurrence of an element from the left array in the right array.
My first task was to find the location where to split the array. For this, the dyadic ⍳ was very useful.
(⌊/ 'do' ⍳⍨ 'Hello World')-1
4
Then it was just a matter of taking and dropping the same amount
(4 ↑ 'Hello World')(4 ↓ 'Hello World')
┌────┬───────┐
│Hell│o World│
└────┴───────┘
The rest of the solution was catching edge cases, and train building.
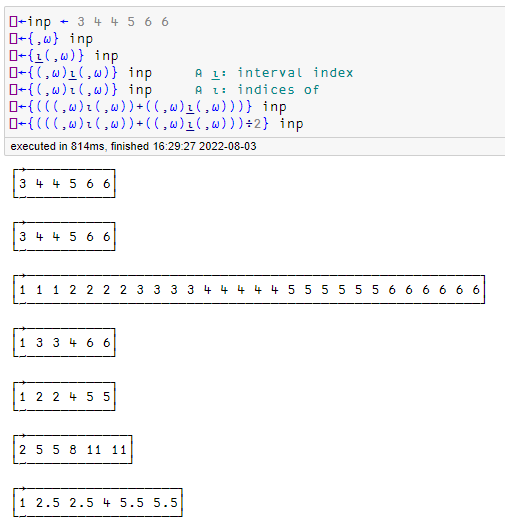
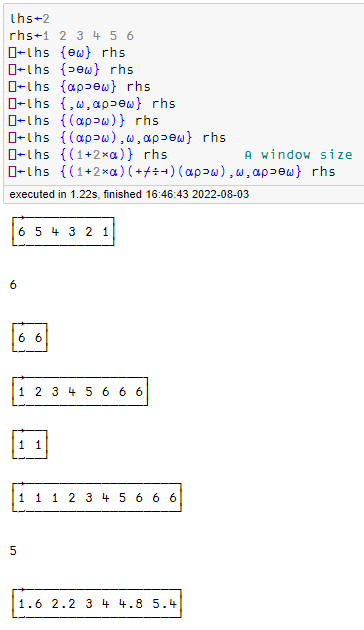
9: An Average Window (or a Windowed Average)
fn ← {n←(1+2×⍺)⋄n÷⍨n+/(⍺/1↑⍵),⍵,(⍺/¯1↑⍵)}
For this problem, I wanted to construct an array with the appropriate padding and then perform the windowed average.
I would need ⍺ extra copies on each end of my array to accommodate a window size of 1+2×⍺.
2 { (⍺/1↑⍵),⍵,(⍺/¯1↑⍵) } ⍳6
1 1 1 2 3 4 5 6 6 6
With such an array constructed, the windowed sum was performed and divided by the window size to calculate the average
2 fn ⍳ 6
1.6 2.2 3 4 4.8 5.4
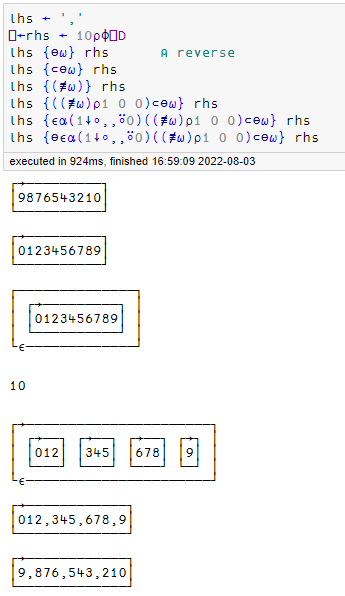
10: Separation Anxiety
fn ← {↑,/ ⍺ {⍺} @ {0=6|⌽⍳≢⍵}1↓(2 ⊂ ⍵)}
My approach here was to split up the input by using a partition enclose. The left argument of the dyadic form represents the number of dividers to place between each element.
{1↓(2 ⊂ ⍵) }'10000000'
┌─┬┬─┬┬─┬┬─┬┬─┬┬─┬┬─┬┬─┐
│1││0││0││0││0││0││0││0│
└─┴┴─┴┴─┴┴─┴┴─┴┴─┴┴─┴┴─┘
With this setup, now we need a function to insert our separators where they belong. We want our separator to be placed at every 6th position, starting from the right, so I reversed an iota and performed a modulo.
{0=6|⌽⍳≢⍵} {1↓(2 ⊂ ⍵)} '100000000'
0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0
With a boolean mask established all we need to pass to the @ operator is the separator and join the result
',' {↑,/ ⍺ {⍺} @ {0=6|⌽⍳≢⍵}1↓(2 ⊂ ⍵)} '100000000'
100,000,000
I am so glad I managed to complete them all with gold tropies although the solutions are sub-optiumal. 
