Hi, I’m working on the section about SGD (An End-to-End SGD Example) and have a few question about the roller coaster example.
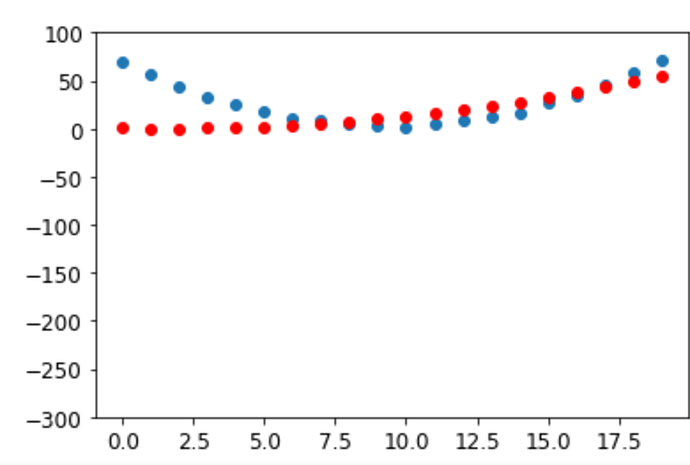
- I run the training (using code from the book) for as many as 50 times and yet, the predictions don’t closely resemblance the actual speed for time 1 through 6 (see attached screenshot, the first 6 red dots). I can’t figure out why the predictions aren’t good.
def apply_step(params, prn=True):
preds = f(time, params)
loss = mse(preds, speed)
loss.backward()
params.data -= lr * params.grad.data
params.grad = None
show_preds(preds)
return preds
for i in range(50): apply_step(params)
- The book code make all predictions, compute all the gradients to adjust all the weights in a single pass. As an experiment, I changed it to train on one data point at a time, as follows:
def epoch_one_input(params):
preds = torch.zeros(len(time))
# Predict one input (i.e. time) at a time and adjust weights
for i in range(len(time)):
preds[i] = f(time[i], params)
preds[i]
loss = mse(preds[i], speed[i])
loss.backward(retain_graph=True)
lr = 1e-5
params.data -= lr * params.grad.data
params.grad = None
show_preds(preds)
for i in range(50):
epoch_one_input(params)
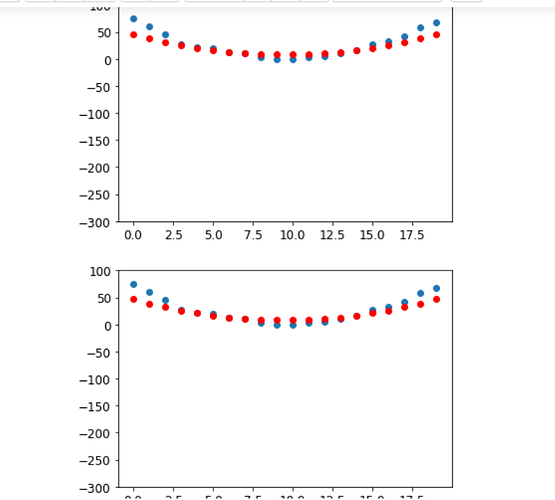
It seems to work, although with the same limitation with the original code (i.e. predictions for time 1 through 6 are always bad). My questions are:
a. Does this code make sense at all or is this not how SGD supposed to work?
b. If it’s okay, what are the advantages and disadvantages of training and adjusting weights for 1 input at a time instead of for the entire set?
c. I need to add retain_graph=True to the loss.backward call or else I would get an error. But why this is not needed for the book’s code even though backward is also called many times?
Thank you and I appreciate any help.