Thanks all! This is released now 
2 Likes
Hey @parrt look!
4 Likes
thanks. I think I fixed that one as well.
What exactly you need?(will need to search for the source link on arvix)
Nevermind. I found it https://arxiv.org/pdf/1603.07285.pdf
1 Like
Yep I was just going to share the link …
Thanks for writing such an amazing and handy paper…
Our pleasure!
I recently joined a Uni to learn the math properly. I think this will become my bible for the next couple years.
Thank you so much Jeremy!
Ooops! Pardon me. And parrt also, huge thanks to both of you!!
Great blog.
Seems there is an error.
Matrix calculus section:
J =… the result matrix; the right bottom cell is 1. But for g(x, y) = 2x+y**8 it should be 2, isn’t it?
quite right. the error I picked up earlier and has been fixed propagated through.
@parrt
fixed. pushed.
I added links to two matrix calculus calculators that can do symbolic differentiation and added a link to arithmetic for convolution.
I am not sure I am reading this right. n is used for the horizontal dimension, thus a default vector (which happens to be horizontal) will be n x 1. This confused me because I am used to matrices being described as m x n where m is the horizontal dimension.
Then in 4.2 we are stating that m = n. I think we do this because we earlier claimed m to be an arbitrary count of functions in a vector. So now we reuse m to make a point that hey, these functions are different from one another and each lives at some location in a vector. Sort of like numpy arrays:
[[f1],
[f2],
[f3]]
And so in this figure on the right we have a vector of element-wise operations that has size n x 1?
So this essentially is
[[f1(w) O g1(x)],
[f2(w) O g2(x)],
[f3(w) O g3(x)]]
where the f functions operate on vector w and g functions on vector x. We are taking a function, evaluating it on its vector and taking a circle of the result. I guess we assume those functions take in a vector and return a scalar? Or both the f and g functions return vectors of same length and we get a matrix?
And in the next diagram we use n in the denominator of the partial derivative symbol… and by the function symbol. But those ns are not the same?
My vector where various f functions live can be of size 5 x 1. And g has to be of size 5 x 1 then. But maybe they only take two arguments each? Or in other words, a vector of length 2.
The Jacobian could then be of size 5 x 2? And n in the denominator =/= n by function name?
Or are we saying that the ns have to be the same. But why?
Hi Radek! I mean nx1 to mean n rows as you suggest, which would make it a vertical vector. I typically use vertical vectors as the default. n is not so much for the horizontal dimension as it is the number of variables, versus the number of functions.
for the element wise operations, yes the result of each fi OP gi is a scalar and so the whole vector is a vertical vector n rose by one column. for the Jacobian I’m really just saying that it is a square matrix because the number of functions equals the number of variables. We are not really talking about a vector of functions but a function of vectors.
I’m not sure if I’m answering your question… does this get us closer to the same ideas? thanks!
Thank you very much for you answer, really appreciate it
Here
f1 =/= f2? Those are different functions?
And we happen to have n of f functions and of g functions, so this works and produces the y vector?
The Jacobian is the result of taking partial derivatives of the results in the y vector with regards to the elements of the w vector? So it will produce a matrix of dimensions |y| rows by |w| columns, and in our case it just happens to be a square matrix? But what if the f functions were scalar valued functions of a vector of length 2? We would than have a Jacobian that would be |y| rows by 2 columns?
It is just by choice that we end up with a square Jacobian but there is nothing inherent in the calculation that makes / requires these to hold?
Unless we are still doing the identity functions Now that I think maybe we are But if we are than in a more general sense the Jacobian doesn’t have to be square?
hiya! f1 and f2 are different functions, yes, In principle. However one can imagine a single function that takes a vector argument. That would map to the same thing. f(x) is same as fi(xi). Yes, f(w) gives a matrix that has |f| rows and |w| columns. in our case it just happens to be square. Yep, the Jacobian would be |y| x 2 columns as you indicate.
Yes, we could have a scalar function with a vector argument f(x), which would give one row and |x| columns. We can also imagine the opposite where we have a vector of functions and a single scalar argument f(x), in which case we would get |f| rose and one column.
the Jacobian definitely does not have to be square. It degenerates to the gradient when there is only a single function.
3 Likes
Ah this is outstanding Thank you very much!!!
Hi @jeremy , your article is very good and I gain a lot. Thanks for your share. But I think there is one error in the section of ‘Vector sum reduction’. The derivative of y=sum(Xz) with respect to scalar variable z should be the sum of X, not n. The first equation is wrong:
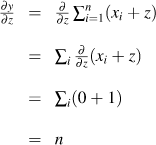
(xi + z) should be xi*z