Hi guys, I’m vaguely understand why we need mean 0 and var 1 weights but can’t come to a clear understanding. Can anybody help with this ?
Hi @qnkhuat, you can get an intuitive understanding by running through the notebook
02b_initializing.ipynb
I’ve looked into it but I think that nb is more about why we need good init than explaining why it needed to be 0 mean and 1 variance. I’ve not find any intuition behind it.
Hi @qnkhuat,
I agree with you; the notebook does demonstrate why we need good initialization. But I’ll push back and point out that it also demonstrates why the key property for a ‘good initialization’ is that it keeps mean and variance of the outputs close to 0 and 1, respectively.
Please have another look at this (refactored) notebook. No need to read all of it, just the sections related to how to get a good initialization.
In the notebook, we see that
(1) If the weights and inputs are initialized randomly from a standard normal distribution, then iteratively applying a linear matrix transformation to the input results in the output mean and sqr blowing up within a few dozen iterations. This is intended to simulate how a deep network behaves, with each iteration representing another layer.
(2) If , on the other hand, we scale the weights by a small number (0.01), mean and sqr tend to approach zero after a few dozen iterations.
(3) We can identify a ‘magic scaling factor’ (Xavier initialization) that, when applied to the initialized weights, keeps the values of mean and sqr near 0 and 1 respectively, under a linear matrix transformation. When hen this new initialization is applied, mean and sqr can remain stable (near 0 and 1 respectively) for 100 layers.
I hope this helps you to see why the initialization of the weights must be chosen so that applying each layer of the network leaves the outputs with zero mean and unit variance.
Hello. If I understand you well, this post on Quora might help, especially the 4th point. In short zero mean and unit variance help gradient descent based optimizers to converge/converge faster.
For anyone working through “Deep Learning From the Foundations”, either on your own or with the TWiML Study Group:
Here are annotated versions of Lesson 9 jupyter notebooks 02b_initializing and 03_minibatch_training
The goal is to help people to understand the notebooks from the top down and from the bottom up. This means explaining:
- tricky, mysterious or unnecessarily terse lines of code
- unfamiliar python or software engineering constructs
- what each cell does, and
- understanding the purpose of the notebook as a whole
If you find that you are struggling, don’t give up. Try to formulate your doubts into a question that, if answered could help improve your understanding. Ask the question on this forum. Never be afraid to ask your question. If you hesitate, thinking that surely everyone else understands, and you don’t want to waste their time with a silly question, consider that:
(1) if you didn’t understand something  , perhaps it’s not you – it’s quite possible that the explanation itself needs clarification
, perhaps it’s not you – it’s quite possible that the explanation itself needs clarification 
(2) more likely than not, others have the same question  , and
, and
(3) asking your question will ultimately help them as well as helping you. 
Questions and Comments are welcome.
Hi @KarlH, Your second form is indeed another way to compute the variance. But let’s think it through: y.std().pow(2) first computes the variance, then takes the square root to get std(), and then squares again to get the variance. This requires two unnecessary extra operations, so it’s wasteful. That’s why the first form, y.pow(2).mean() is preferable.
Remember that the weights are not yet normalized before Softmax is applied. What happens when the weights of the two pixels differ by a constant offset? i.e. What happens when each pixel 2 weight is d units different from the corresponding pixel 1 weight, where d is a constant?
When you transform the weights by exponentiation, a constant offset d between two sets of weights becomes a multiplicative factor.
To see this, suppose that the weights of pixel 1 are
w_1,w_2
and the weights of pixel 2 differ from those of pixel 1 by an offset d, so that they are
w_1+d,w_2+d
The exponentiated weights for pixel 1 are
\exp{w_1},\exp{w_2}
And the exponentiated weights for pixel 2 are
\exp{(w_1+d)},\exp{(w_2+d)} = k\exp{w_1},k\exp{w_2},
where k = \exp{d}.
Now for each pixel, Softmax normalizes the exponentiated weights by their sum, and since
the weights of pixel 2 are proportional to those of pixel 1 by a multiplicative factor of k,
the normalized exponentiated weights will be the same for the two pixels. This is exactly what happens in the example Jeremy discusses in Lesson 10.
Hi. The problems with softmax are addressed by Jeremy in Lesson 10.
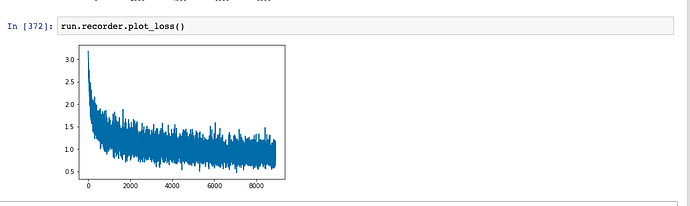
When training my model using the Runner class and trying to plot the losses I’m getting the following graph:
I know Jeremy explained at some point what’s happening when the losses start fluctuating like that and how to tackle it but I just can’t find it.
Can someone help me out? Thanks in advance.
I could not get the lesson transcript search to work. (Nothing happens.) The discussion of softmax characteristics and limitations, though, is somewhere in that Lesson.
If you go here
https://course.fast.ai/videos/?lesson=10
there are some notes on Softmax in the Lesson notes link in the right hand panel. HTH, Malcolm
Found it! @jeremy discusses Softmax starting at 44:38 in Lesson 10 video, and ending at 52:44. He’s discussing the entropy_example.xlsx spreadsheet and the section labelled Softmax in the 05a_foundations.ipynb notebook.
Two key points @jeremy makes are that Softmax operates under the assumption that each data point belongs to exactly one of the classes, and that Softmax works well when these assumptions are satisfied.
However, the assumptions are not satisfied for
(1) multi-class, multi-label problems where a data point can be a member of more than one class (i.e. have more than one label), or
(2) missing label problems where the identified classes do not provide a complete representation of the data, i.e. there are data points that belong to none of the classes.
So what to do about these cases?
@jeremy shows empirically that for multiclass, multilabel problems a better approach is to create a binary classifier for each of the classes.
For missing label problems, @jeremy says that some practitioners have tried
(A) adding a category for none-of-the-above, or alternately
(B ) doubling the number categories by adding categories for not(each class).
However, he says that both of these approaches are terrible, dumb and wrong, because it can be difficult to capture features that describe these ‘negative’ categories.
While I agree that the ‘negative class’ features could be hard to capture, I’m not convinced that either of the approaches (A) and (B) are wrong, since in each case, the classes satisfy the Softmax assumptions.
Case (A): if you can learn what features are present in a certain class K, you also know that when these features are absent, the data is not likely to be a member of class K. This means that learning to recognize class K is implicitly learning to recognize class not(K).
Case (B) I’d argue that none-of-the-aboveness can be learned with enough examples.
So I don’t see anything wrong with these approaches to handle the case of missing classes.
To summarize, Softmax works well when its assumptions are satisfied, and gives wrong or misleading results otherwise. An example of the former case: Softmax works well in language modeling when you are asking “what’s the next word?” An example of the latter case is when there are missing classes and you don’t account for this situation by using, say approach A or B above; in this case the output probabilities are entirely bogus. Multiclass, multilabel problems provide another example where Softmax is the wrong approach, because the class probabilities do not sum to one.
The Lesson 9 notebook 02_initializing.ipynb contains an enlightening series of experiments that empirically derive a ‘magic number’ scale factor for effective random Gaussian initialization of a linear layer followed by a ReLU.
In this annotated version of the notebook, 02b_initializing_jcat, I explore verifying the notebook’s empirical results from first principles.
The first experiment computes the first and second moments (mean, sqr) for a
Linear transformation of a scalar input, followed by a ReLU
Here is the original code cell
which calculates (mean, sqr) empirically as (0.321, 0.510)
In the section What just happened? immediately following that code cell, we compute
(mean, sqr) from first principles and show agreement with the empirical results.
The original notebook then goes on to extend the scalar example to a
Linear matrix transformation of a vector input, followed by a ReLU
Here is the section that computes the empirical result, which turns out to be
(mean, sqr) = (9.035, 256.7)
When I applied the same straightforward methodology as for the scalar case, I was surprised to find that the calculation for mean did not agree with the empirical result. I’m perplexed, still trying to understand where I went wrong.
Perhaps someone can help set me straight?
They’re mathematically doable. But I think the “with enough examples” is a clue as to the issue here - in general, we want an architecture that is as easy to learn as possible. My guess is that “does not look like any of {n classes}” might be hard to learn. And doubling the number of categories at the very least doubles the # params in the last layer - but then also needs enough computation in earlier layers to drive these.
Anyhoo, this is all just intuition - so if someone want to try some actual experiments, that would be very interesting! 
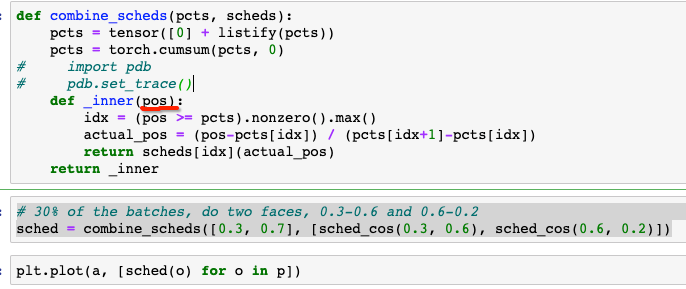
I don’t get how is pos being transferred here. I get that 0.3 and 0.7 represents it, but how is it getting to _inner ?
Thanks !
0.3 and 0.7 are saying use 30% of the budget to go from 0.3 to 0.6 of a cosine scheduler and 70% of the budget to go from 0.6 to 0.2 of a cosine scheduler.
combine_scheds is a function that returns the function _inner. (last line - return -inner)
so combine_scheds is returning _inner that takes the pos argument.
now when you say - sched = combine_scheds([0.3, 0.7], [sched_cos(0.3, 0.6), sched_cos(0.6, 0.2)])
sched is this _inner function which takes pos.
next you say - plt.plot(a, [sched(o) for o in p]) , here sched(o) is like _inner(o) where o is the pos that is expected.
previously p was defined as p = torch.linspace(0.01,1,100) and this is what you are passing to sched which is passing it to _inner. Hope that helps !!! 
helps alot ! thanks !
p = torch.linspace(0.01,1,100)
pcts=[0.3, 0.7]
pcts = tensor([0] + listify(pcts))
pcts = torch.cumsum(pcts, 0)
for i,o in enumerate(p):
idx = (o >= pcts).nonzero().max()
actual_pos = (o-pcts[idx]) / (pcts[idx+1]-pcts[idx])
print(i,o, idx,actual_pos)
rewriting the same piece of code, now you can print and see the values.
scheds = [sched_cos(0.3, 0.6), sched_cos(0.6, 0.2)]
scheds[0](0.5)
you are combining two cos functions smoothly and the condition is that you want it start at 0.3 and go up to 0.6(for 30%) and then back down to 0.2(for 70%). (these are the y values on the graph)
So you basically have those three points. But you don’t know where the corresponding x values for these points are. This is controlled by what percentage you allocate to each of the schedulers.
pcts = [0.3,0.7] - first 30% sched_cos(0.3, 0.6) and last 70% sched_cos(0.6, 0.2)
pcts = [0.0,0.3,1.0] , because of the cumsum
starting point - sp; ending point - ep
for scheduler1: sp =0, ep =0.3
for scheduler2: sp =0.3, ep =1.0
actual_pos =( x - starting_point) / (ending_point - staring_point)
Hope that helps.