Jeremy will give one later, but this is obviously a new hyperparameter to adjust.
The bias is just another weight for the model. It gets updated during gradient descent.
8 Likes
Is bias here a bit like the average rating a user gives independent of the latent movie features, and the average rating a movie gets independent of the latent movie features
2 Likes
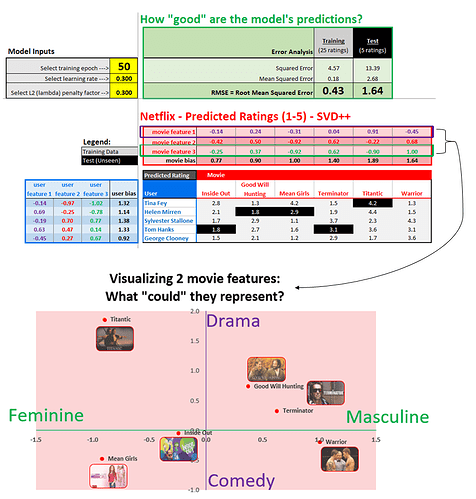
Here’s an illustrative latent factor visualization from my Excel model (inspired from Jeremy’s lesson - see Part 4 of this blog post):
25 Likes
Yes a bit of that. It’s the harshness of the user and the value (in one sense) of the movie.
2 Likes
So the cycle is over all the epochs you specified in fit_one_cycle right ?
Why sometimes I am getting negative value of loss and negative value of validation while training? What is the intuition of negative loss?
12 Likes
Exactly.
1 Like
This is a great blog post - I really recommend it!
2 Likes
We embed a movie or a user using 4 numbers. Why not 10? Is that a hyper-parameter?
In general it is the ‘absolute level’ of that item relative to other items. In this case, your intuition is correct.
can some one explain div factor used in fit on e cycle
Yes, the embedding size, also called in this instance, the number of latent factors.
2 Likes
When we visualise kernels in CNN, what are we plotting? The weights of those kernels or activations?
A bit late, but why replace the later weight matrix of ResNet by 2 matrices with a ReLu in between, instead of just 1 matrix?
What does that bring?
2 Likes
Does an epoch train on all the whole training set or only a single batch?
Are binary variables worth being represented by embeddings?
fit one cycle will change your learning rate according to the one cycle policy. This means that you will start with a smaller learning rate lr/div go to lr and then go back. The best way is to see that with plot. You will get instantly.
If you say div = 10, your starting learning rate is 1/10 the lr you set.
1 Like
This is not equivalent because ReLU is non-linear. The universal approximation theorem tells us we can model anything as long as we use affine transforms with non-linearity between them.
6 Likes
On whole training set.