You generally have to write gpu compiled code(kernels) for the gpu, to run code on them. Kernels have to be written in a way that is aware of the GPU architecture, such as parallelization, memory layout, or suffer huge performance penalties.
2 Likes
How does python know which axis to use to broadcast?
Some Resources on numpy and pytorch broadcasting:
10 Likes
There are exact rules for this, see the numpy docs.
1 Like
Can someone clarify when to use None indexing into a tensor (like this tensor[...,None]) in order for broadcasting to work; we didnât need it for that mnist_distance function in the notebook when I thought we would have.
1 Like
Are all tensor broadcast operations run on GPU ? Or are there special GPU tensor broadcast operations that we have to code. Also what could be an easy way to performance test the difference of running tensor broadcast operations on the cpu vs the gpu.
Look at the rules of numpy broadcasting. This None adds a fake axis with a dimension of 1, which will trigger a different behavior (you probably need to experiment with it tomorrow to fully understand 
)
2 Likes
Tensors have a device which is either CPU or GPU. If the tensor is on the GPU, the broadcasting will happen there (otherwise not).
3 Likes
put %timeit in your jupyter cell to measure the time required to a particular cell. Here it a link %timeit in python
4 Likes
There is overhead for running on gpu, so you may have to increase batch size to see a performance improvement on a gpu.
3 Likes
Am I right in understanding that the âpredictâ function is y=mx+b which we are trying to find based on the universal approximation for our specific task? With an aim to find the best m and b using SGDâŚ?
4 Likes
Thatâs it, in a nutshell.
4 Likes
Shouldnât the slope at the point shown be negative?
Why not using the 2nd derivative to choose the steps?
In practice, we have a model with millions of parameters. The gradients are the same size so can fit in memory, but the second order derivatives are of that size squared⌠so waaaaay too big to fit in memory, And very expensive to compute.
But in an ideal world, yes. That would give something as fast as Newtonâs method.
16 Likes
Thatâs a flag that we are on the left side and we not quite there at bottom based on the function presented. Thatâs when the weights will be updated and move away from there. I like to think of it as changing the direction and amount to get at a point where the loss is 0 or close to there. Hence, gradient descent.
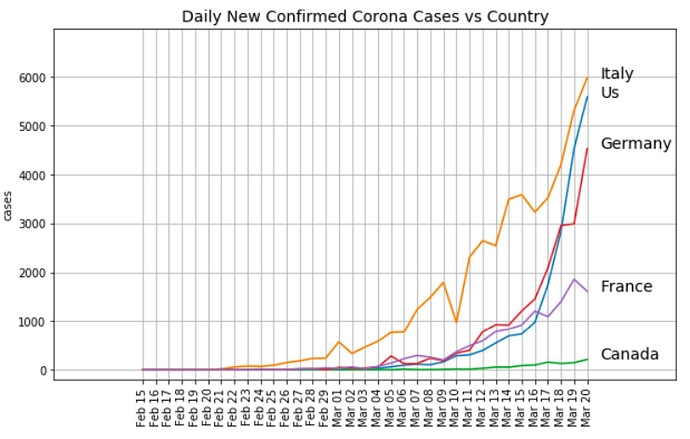
Last week I saw another Corona cases graph which, as I expected, also showed the exponential increase (broken out by country). Then I had a closer look: wait a minute, this graph shows the âdailyâ new cases, not the âtotalâ new cases. How can the daily new cases graph also look exponential? I expected something increasing, but not exponential as in the âtotalâ graphs. Then I realized: of course, the derivative of an exponential function is also exponential!
5 Likes
Guess params is None. Can check why
Itâs a litte more complicated than that. In reality, the spread of an infectious disease like COVID-19 is going to be a logistic function (sigmoidal). The derivative is actually a logistic distribution function. When we talk about flattening curve, we mean flattening the logistic distribution function!
(itâs a misconception that the curve is actually a Gaussian bell curve)
1 Like