I have been thinking about this a bit and also some time ago in BetterExplained books I read this interesting take on exponents being likened to microwave ovens which led me to this…
If we have cars and would like to know what fitting an AC will do to its price in absolute terms - how many dollars more it will be worth - we would just use prices in dollars.
But then it is as if we were saying that whether we stick an AC in a jaguar or in a Fiat 126p

(Tom Hanks seems to have a thing for them though do not know the whole story)
we would want to be able to predict the difference in value - here 1000$ more and here 1000$ doesn’t make sense (you can buy 1/60 of a jag for 1000$ and probably like 3 or 4 fiats 126p ![]() )
)
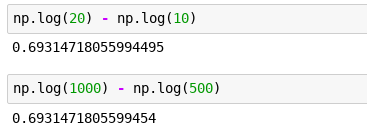
So we ask a different question - with respect to the base price, how much will fitting an AC increase it? 0.1 on the logarithmic scale will ‘grow’ both values by the same amount relative to their starting magnitude!
Maybe this has some more significance that I fail to notice yet and also apologies if this was explained in a lecture already but I am a bit behind, even more so on the notebooks than watching the lectures.
This is crazy:
Here, have 40$, can you grow it for me by half?
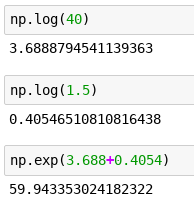
ah wait… but I’d like you to grow it by half… and then by half again… (this mimics getting an AC and then adding a set of rims onto the cars / bulldozers which prices we are are predicting)
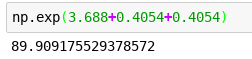
0.4054 always adds a half!!! OMG I can’t believe I didn’t know that.
BTW this logarithmic thing is witchcraft.