Understanding the Tiramisu Architecture

brookisme · April 3, 2018, 4:04am

Hi Everyone - I am trying to use the Tiramisu architecture for a project and the closer I look at the paper I realize I didn’t quite understand things the first time around.

This is a pretty detailed post but hopefully someone whose spent some time thinking about this architecture won’t mind digging in.

I have 2 questions, that are probably related.

Q1: Transition Up

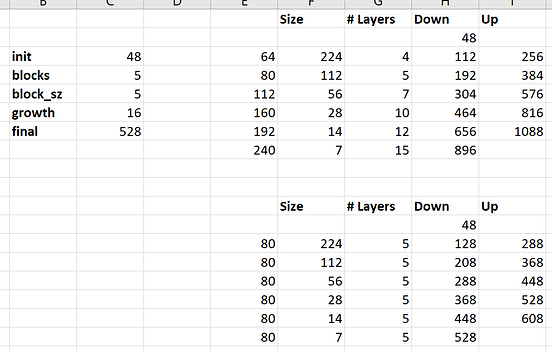
My main confusion lies in the transition-up feature maps. In Table 2 of the paper they explain the architecture layer-by-layer including the number of feature maps at the end of each block.

The down path, “DB+TD”, are easy to understand. If the input to the DB+TD has n features:

The output of the DB has growth_rate*(# of layers) features
The output is then concatenated with the input to the DB giving (n+growth_rate*(# of layers))
The TD-conv preserves the number of features.

These steps can easily be show to reproduce the DB+TD parts of this table.

However, moving on to the bottleneck. The output of a dense-block (as above) is simply growth_rate*(# of layers) in this case 16*15=240. Note the input to the bottleneck output, 656, plus the output of the dense-block does give 896, however there is not a concat after the bottleneck so it seems it should be 240.

“TU+DB” has the same problem. Since it ends in a DB the outputs should have growth_rate*(# of layers). Maybe they meant “previousDB+TU” or “previousDB+TU+(concat with skip connection)” which would allow us to pick the number of filters in the TU to give the m they list here but i feel like I am missing something.

Q2: Dense Block

I think I found a mistake in an old notebook of Jeremy’s but chances are its my mistake and is wrapped up in my confusion above - actually we both seem to be right depending on what part of the paper you read.

I stated above that the output of the DenseBlock has (k*l) feature-maps where k is the growth rate and l is # of layers. This is because the output of the dense-block is the concatenation of the l layers and each layer contains a conv with “k” filters. The output of the dense-block is then concatenated with the input to the dense-block giving “m + k*l” features. This is clearly illustrated in Figure 2, and described in the caption of Figure 2 (see Fig 1 for the concat).

However in the old version keras-based fastai course Jeremy didn’t concatenate the layers to get the output of the dense-block but rather concatenated the output of the last layer with the input of the last layer. See input 47 of this notebook.

This seems to clearly contradict Figure 2. However the last paragraph of section 3.1 seems to describe what Jeremy has reproduced in his notebook.

Thanks for making it this far!

brookisme · April 3, 2018, 4:52pm

I realized I should have mentioned a suspected typo in Table 2 included above:

Even though I am confused about them, the m values for the TU+DB layers can (with one exception) be reproduced with

k*l + in_f + skip_f

Where:

k: is the growth-rate
l: is the number of layers
in_f: is the number of feature-maps in the input
skip_f: is the number of feature-maps in the skip-connection that the output of the TU is concated with

This is true for every instance except the 7-layer (m=578) row. In that case the above formula gives 576. I am guessing this is simply a typo.

brookisme · April 3, 2018, 5:39pm

One final update. Assuming I haven’t messed up my architecture I realized there was a final hack to try and deduce how to choose the number of filters in the transition-up: Try a different of options and compare the number of parameters to the number of params given in Table 3 at the end of the paper. I tried the following:

So that the output of the TU matches the number given in Table 2
So that the output of the concat(TU,skip) matches the number given in Table 2
So that it preserves the number of feature-maps (ie the number of feature-maps of the input to the TU)
three more random choices involving the growth-rate, depth, input-nb-fmaps,…

Preserving the number of feature maps gives the correct number of params (9.4 million for DN103)

The others were way off - most over 11 million - one random option 8.9 million.

Take aways:

Yay! The sensible answer appears to be the right one. Preserving the number of feature-maps is what I did originally, before looking at closely at Table 2.
The question still remains - what are the “m” values in Table 2.
This might be an indication that concat-ing the layers for the output of the dense-block (as described in Fig 2) was the correct approach - as opposed to simply concat-ting the input and output as done in @jeremy’s notebook (as described at the end of section 3.1).

On that last point - who knows maybe they both have 9.4m params or maybe the 9.4m is a coincidence and none of this is right, but I doubt it. I’m guessing the conflicting text, and figure/caption is because the authors tried both things.

jeremy · April 3, 2018, 6:49pm

FYI I created a spreadsheet back when I worked on this - dunno if this helps:

I vaguely remember there was a error in the table in the paper…

brookisme · April 4, 2018, 5:00am

Thanks @jeremy - I’m still a bit confused on how what they’ve described in the paper matches up with Table 2 but your chart made me take second (… well 15th) look. Looking closer at your tiramisu (actually @bckenstler’s where’s waldo tiramisu).

I realized a couple things:

My down-block ends with the concat of all the layers, and then there is a concat outside of the dense-block to form a skip connection this matches up with Fig 1. It also means i have a concat layer followed by a concat layer. Additionally I have an explicit bottleneck (which differs from the down block because there is not an exterior concat). A layer by layer comparison things look different, but these super large networks have the exact same number of parameters and I think we are ultimately doing the same thing.
On your up path you are passing on your added layer which is exactly the “concat of all layers” i spoke about above, so in the up path we are doing the same thing in the same way. However at the end of your network, the output of the up-path is the “x” layer not the “added” layer – I had been returning the “added” layer, and in fact - when I said the parameters were the same in the two networks above, this is only true if i swap the output of the up-path to be your “x”.

I’m still not 100% sure what the authors intended, but I’m feeling more confident. At this stage, I’m going to try a couple small variations and see which works best.

Thanks again.
Cheers,
Brookie

jeremy · April 4, 2018, 10:34am

I’ll be interested to hear what you find!