Trying to make sense of GAN losses

Deep Learning
1

Hello, from this paper I’m trying to map this equation:
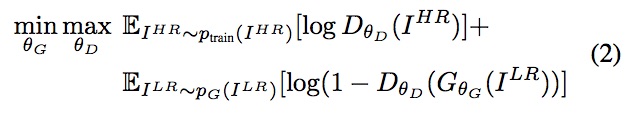
1609_04802_pdf

To my pytorch code. If I understand this right:

  • E_i^hr~P_train(I^hr) is entropy that the data from real distribution (P_train(I^hr)) passes through the discriminator with I^hr being the hr_images in the code below
  • E_i^lr~P_G(I^hr) is entropy that the data from real distribution (P_G(I^hr)) passes through the generator with I^lr being the lr_images in the code below

So basically I have this:

sr_images = self.netG(lr_images) # Generator output
d_hr_out = self.netD(hr_images)  # Discriminator Sigmoid output
d_sr_out = self.netD(sr_images)  # Discriminator Sigmoid output

d_hr_loss = F.binary_cross_entropy(torch.log(d_hr_out), torch.ones_like(d_hr_out))
d_sr_loss = F.binary_cross_entropy(torch.log(1- d_sr_out), torch.zeros_like(d_sr_out))
d_loss = d_hr_loss + d_sr_loss # Discriminator loss

Does it looks correct to you? Or am I missing something. Thank you.

The whole code (not up to date)

2

The discriminator is trying to correctly classify both the real and fake so you need those 2 elements and then take a gradient step
D_loss_real = nn.binary_cross_entropy(D_hr_out, ones_label)
D_loss_fake = nn.binary_cross_entropy(D_sr_out, zeros_label)
D_loss = D_loss_real + D_loss_fake

And then take a gradient step with generator
G_loss = nn.binary_cross_entropy(D_sr_out, ones_label)

2 Likes