I am not sure if this fits the ‘theory’ category of this forum, but my question is about the theory in principle.
To learn more about neural networks, I created a toy example for a non-linear regression task , using Pytorch. The problem is that the network never learns the function in a satisfactory way, even though my model is quite large with multiple layers (see below). Or is it not large enough or too large? How can the network be improved or may be even simplified to get a much smaller training error?
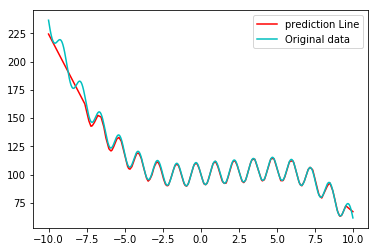
I experimented with different network architectures, but the result is never satisfactory. Usually the error is quite small within the input interval around around 0 (see image below), but the network is not able to get good weights for the regions at the boundary of the interval (see plots below). I could generate even more training data, but I have not yet understood completely, how the training can be improved (tuning parameters such as batch size, amount of data, number of layers, number of neurons, epochs etc.)
For the moment I do not care too much about overfitting, my goal is to understand, why a certain network architecture/certain hyper parameters need to be chosen. Of course, avoiding overfitting at the same time would be a bonus.
Of course, using the learning rate finder of fast.ai would be nice, but I am not sure how to implement it in pure Pytorch (or implementing my model in fast.ai).
I have watched most of the fast.ai course part1.v2, but I am especially interested in using neural networks for regression tasks or as function approximators. In principle my problem should be able to be approximated to arbitrary accuracy by a single layer neural network, according to the universal approximation theorem, isn’t this correct?
Thanks for any hints 
import torch
import torch.utils.data as utils_data
from torch.autograd import Variable
import numpy as np
from torch import nn, optim
import matplotlib.pyplot as plt
#This is the function the neural network should learn:
def my_funct(x_input):
y = 0.5*x_input**2 + np.cos(x_input) - 10*np.sin(5*x_input) - 0.1*x_input**3 +x_input + 100
return y
# Here I create the training data:
x_train = np.random.uniform(low=-10, high=10, size=23500)
y_train = my_funct(x_train)
x_train = x_train.reshape(-1,1)
y_train = y_train.reshape(-1,1)
batchsize = 32
training_samples = utils_data.TensorDataset(torch.from_numpy(x_train), torch.from_numpy(y_train))
data_loader = utils_data.DataLoader(training_samples, batch_size=batchsize, shuffle=False)
# Create the model in Pytorch:
D_in, H_1,H_2,H_3,H_4, H_5,H_6, D_out = 1, 80,70,60, 40,40,20, 1
model = torch.nn.Sequential(
torch.nn.Linear(D_in, H_1),
torch.nn.ReLU(),
torch.nn.Linear(H_1, H_2),
torch.nn.ReLU(),
#torch.nn.BatchNorm1d(H_2),
torch.nn.Linear(H_2, H_3),
torch.nn.ReLU(),
#torch.nn.BatchNorm1d(H_3),
torch.nn.Linear(H_3, H_4),
torch.nn.ReLU(),
#torch.nn.BatchNorm1d(H_4),
torch.nn.Linear(H_4, H_5),
torch.nn.ReLU(),
torch.nn.Linear(H_5, H_6),
torch.nn.ReLU(),
torch.nn.Linear(H_6, D_out),
)
criterion = nn.MSELoss()
#optimizer = optim.SGD(model.parameters(), lr=1e-4, momentum=0.8)
optimizer = optim.Adam(model.parameters())#, lr=1e-3, momentum=0.8)
model.train()
num_epochs = 100
loss_list = []
for epoch in range(num_epochs):
for batch_idx, (data, target) in enumerate(data_loader):
#print(batch_idx)
data, target = Variable(data), Variable(target)
optimizer.zero_grad()
output = model(data.float())
loss = criterion(output, target.float())
#print(batch_idx, loss.data[0])
loss.backward()
optimizer.step()
if epoch >2:
if batch_idx % 200 == 0:
loss_list.append(loss.data[0])
if batch_idx % 400 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(data_loader.dataset),
100. * batch_idx / len(data_loader), loss.data[0]))
x_train = torch.from_numpy(x_train).float()
y_train = torch.from_numpy(y_train).float()
# plot the predictions and the difference
model.eval()
prediction = model(Variable(torch.Tensor(np.linspace(-10,10, 10000).reshape(-1,1))))
prediction = prediction.data.numpy()
plt.plot(np.linspace(-10,10, 10000), prediction, c= 'r', label='prediction Line')
plt.plot(np.linspace(-10,10, 10000), my_funct( np.linspace(-10,10, 10000) ), c='c', label='Original data')
plt.legend()
plt.show()
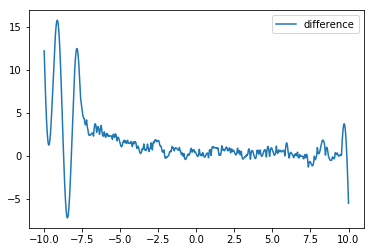
plt.plot(np.linspace(-10,10, 10000), my_funct( np.linspace(-10,10, 10000))- prediction.ravel(), label='difference' )
plt.legend()
plt.show()
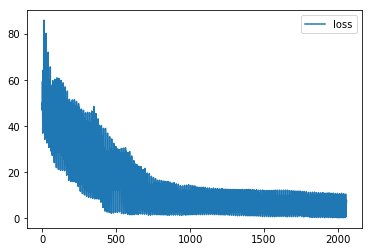
plt.plot(loss_list, label='loss')
plt.legend()
plt.show()