Unofficial Deep Learning Lecture 5 Notes
Hi All,
Please find the lecture 5 notes. There was a lot of great material covered today, so hoping you guys can flesh out some of the details. I tried to capture as much as I could, but there was a lot of math to absorb near the end of the lecture around the topics of momentum + Adam optimizer.
Hope the notes are useful!
Cheers,
Tim
@jeremy please convert to wiki, so all can contribute? Thanks ahead of time, great lecture today.
Today we are going to start the second part of this course. Now, what we now going to do is go in reverse. We are going to go back over all of those exact same things again but this time we are going to dig into the detail of every one and we are going to look inside the source code of fastai library to see what it’s doing and try to replicate that. So, in a sense like there’s not going to be a lot more best practices to show us like Jeremy have kind of shown us the best best practices that he knows. Jeremy thinks it’s time for us to now build on top of those, to debug those models, to come back to part 2 where we’re going to kind of try out some new things. It really helps to understand what’s going on behind the scenes.
MovieLens
The goal here today is we’re going to try and create a pretty effective collaborative filtering model almost entirely from scratch. We will use PyTorch as a automatic differentiation tool and as a GPU programming tool and not very much else. We’ll try not to use its neural net features. We’ll try not to use fastai library anymore than necessary.
Let’s look at collaborative filtering. We are going to look at Movielens dataset. The Movielens dataset is basically is a list of movie ratings by users.
We go through the Jupyter notebook here.
If you need to download the dataset:
# !wget http://files.grouplens.org/datasets/movielens/ml-latest-small.zip
# !unzip ml-latest-small.zip
Import the libraries:
%reload_ext autoreload
%autoreload 2
%matplotlib inline
import torch
from fastai.learner import *
from fastai.column_data import *
path='ml-latest-small/'
ratings = pd.read_csv(path+'ratings.csv')
ratings.head()
| userId | movieId | rating | timestamp | |
|---|---|---|---|---|
| 0 | 1 | 31 | 2.5 | 1260759144 |
| 1 | 1 | 1029 | 3.0 | 1260759179 |
| 2 | 1 | 1061 | 3.0 | 1260759182 |
| 3 | 1 | 1129 | 2.0 | 1260759185 |
| 4 | 1 | 1172 | 4.0 | 1260759205 |
movies = pd.read_csv(path+'movies.csv')
movies.head()
| movieId | title | genres | |
|---|---|---|---|
| 0 | 1 | Toy Story (1995) | Adventure|Animation|Children|Comedy|Fantasy |
| 1 | 2 | Jumanji (1995) | Adventure|Children|Fantasy |
| 2 | 3 | Grumpier Old Men (1995) | Comedy|Romance |
| 3 | 4 | Waiting to Exhale (1995) | Comedy|Drama|Romance |
| 4 | 5 | Father of the Bride Part II (1995) | Comedy |
Create subset for Excel
We create a crosstab of the most popular movies and most movie-addicted users which we’ll copy into Excel for creating a simple example. This isn’t necessary for any of the modeling below however.
g=ratings.groupby('userId')['rating'].count()
topUsers=g.sort_values(ascending=False)[:15]
g=ratings.groupby('movieId')['rating'].count()
topMovies=g.sort_values(ascending=False)[:15]
top_r = ratings.join(topUsers, rsuffix='_r', how='inner', on='userId')
top_r = top_r.join(topMovies, rsuffix='_r', how='inner', on='movieId')
# pd.crosstab(top_r.userId, top_r.movieId, top_r.rating, aggfunc=np.sum)
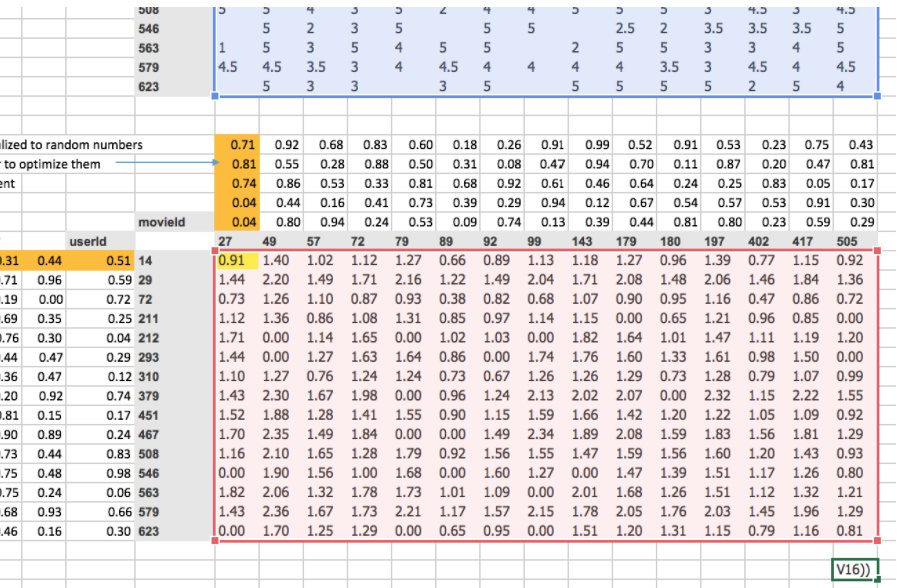
Given some ratings:

Every rating is represented as a matrix cross product (random init)

Note that Microsoft Office for Windows has add-ins. You can turn on the “solver” in the add-ins. This will run an iterative solver.
Now we can calculate the loss

And we can then optimize the ORANGE cells based on the loss, BLUE cells - RED cells.
Collaborative Filtering - High Level
Get a validation indexes
-
wd- L2 regularization -
n_factors- embedding sizes
val_idxs = get_cv_idxs(len(ratings))
wd=2e-4
n_factors = 50
ratings.csvuserIdmovieId-
rating- dependent variable
This movie and user, which other movies are similar to it, which people are similar to this person?
cf = CollabFilterDataset.from_csv(path, 'ratings.csv', 'userId', 'movieId', 'rating')
- size embedding
- index
- batch size
- which optimizer
learn = cf.get_learner(n_factors, val_idxs, 64, opt_fn=optim.Adam)
Run the fit
learn.fit(1e-2, 2, wds=wd, cycle_len=1, cycle_mult=2)
[ 0. 0.84641 0.80873]
[ 1. 0.78206 0.77714]
[ 2. 0.5983 0.76338]
math.sqrt(0.776)
0.8809086218218096
preds = learn.predict()
y=learn.data.val_y[:,0]
sns.jointplot(preds, y, kind='hex', stat_func=None);

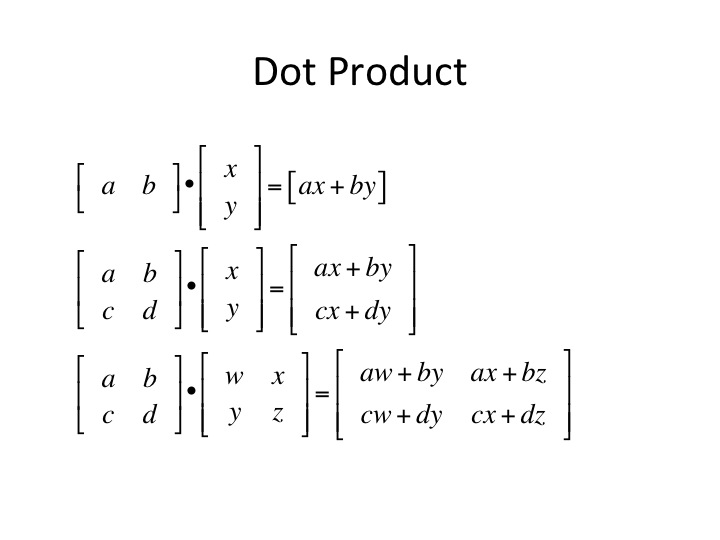
PyTorch and Linear Algebra: Dot product example

T = tensor in Torch
a = T([[1.,2],[3,4]])
b = T([[2.,2],[10,10]])
a,b
(
1 2
3 4
[torch.FloatTensor of size 2x2],
2 2
10 10
[torch.FloatTensor of size 2x2])
a*b
2 4
30 40
[torch.FloatTensor of size 2x2]
(a*b).sum(1)
6
70
[torch.FloatTensor of size 2]
Our First Custom Layer in PyTorch
We are now making a basic Torch class. We are extending the nn.Module from PyTorch
forward is a inherited method from the nn.Module, which is leveraged by other functions in other pytorch libraries
-
forward<- matrix multiplication -
backwards<- gradients
class DotProduct(nn.Module):
def forward(self, u, m): return (u*m).sum(1)
Create an instance of the class
model=DotProduct()
model(a,b)
6
70
[torch.FloatTensor of size 2]
Prepare the data:
- look at unique values of user_ids
- make a mapping from user_id to a INT (so there’s no skipping of numbers)
- do the same for movie ids
Reminder:
-
enumerate- takes in a collection, gives back the index, value for a collection -
lambda- python keyword for making a temporary function
u_uniq = ratings.userId.unique()
user2idx = {o:i for i,o in enumerate(u_uniq)}
ratings.userId = ratings.userId.apply(lambda x: user2idx[x])
m_uniq = ratings.movieId.unique()
movie2idx = {o:i for i,o in enumerate(m_uniq)}
ratings.movieId = ratings.movieId.apply(lambda x: movie2idx[x])
n_users=int(ratings.userId.nunique())
n_movies=int(ratings.movieId.nunique())
Now lets make a more complicated Embedding Layer
-
__init__- this function is called when the object is created. Called the constructor -
obj = myClass()
-
obj = newClassImade(list)
-
nn.Embedding- a pytorch object -
self.u.weight.data- initializing the user weights to a reasonable starting place -
self.m.weight.data- initializing the movie weights to a reasonable starting place -
uniform_- note that_means ‘inplace’ instead of returning a variable and doing an assignment
for forward
- users,movies = cats[:,0],cats[:,1]
We are pulling both datasets out of the categorical variable.
class EmbeddingDot(nn.Module):
def __init__(self, n_users, n_movies):
super().__init__()
self.u = nn.Embedding(n_users, n_factors)
self.m = nn.Embedding(n_movies, n_factors)
self.u.weight.data.uniform_(0,0.05)
self.m.weight.data.uniform_(0,0.05)
def forward(self, cats, conts):
users,movies = cats[:,0],cats[:,1]
u,m = self.u(users),self.m(movies)
return (u*m).sum(1)
Prep the features and dependent variable
x = ratings.drop(['rating', 'timestamp'],axis=1)
y = ratings['rating']
Pull from a dataframe, with x, y, note that we bind the categorical variables together
data = ColumnarModelData.from_data_frame(path, val_idxs, x, y, ['userId', 'movieId'], 64)
Setup a optimizer
-
optim- gives us an optimizer. -
model.parameters()this is inherited from thenn.Module. -
1e-1- is the learning rate -
weight decay- regularization momentum
wd=1e-5
model = EmbeddingDot(n_users, n_movies).cuda()
opt = optim.SGD(model.parameters(), 1e-1, weight_decay=wd, momentum=0.9)
Note: we are not using a Learner, we are using the low-level PyTorch fit.
fit(model, data, 3, opt, F.mse_loss)
[ 0. 1.68932 1.64501]
[ 1. 1.08445 1.30609]
[ 2. 0.91446 1.23001]
### Set the learning rate
set_lrs(opt, 0.01)
fit(model, data, 3, opt, F.mse_loss)
[ 0. 0.69273 1.14723]
[ 1. 0.72746 1.1352 ]
[ 2. 0.67176 1.12943]
Bias
min_rating,max_rating = ratings.rating.min(),ratings.rating.max()
min_rating,max_rating
(0.5, 5.0)
Let’s improve our model
Can we squash the ratings between 1 and 5?
With the sigmoid function we can multiply by our target range

F - its the pytorch functional. its a large library of functions used in deep learning
def get_emb(ni,nf):
e = nn.Embedding(ni, nf)
e.weight.data.uniform_(-0.01,0.01)
return e
class EmbeddingDotBias(nn.Module):
def __init__(self, n_users, n_movies):
super().__init__()
(self.u, self.m, self.ub, self.mb) = [get_emb(*o) for o in [
(n_users, n_factors), (n_movies, n_factors), (n_users,1), (n_movies,1)
]]
def forward(self, cats, conts):
users,movies = cats[:,0],cats[:,1]
um = self.u(users)* self.m(movies)
## add in user bias and movie bias
## squeeze is going to be broadcasting, this will replicate a vector
## and add it to the matrix
res = um.sum(1) + self.ub(users).squeeze() + self.mb(movies).squeeze()
## this limits the range of the ratings
res = F.sigmoid(res) * (max_rating-min_rating) + min_rating
return res
wd=2e-4
model = EmbeddingDotBias(cf.n_users, cf.n_items).cuda()
opt = optim.SGD(model.parameters(), 1e-1, weight_decay=wd, momentum=0.9)
fit(model, data, 3, opt, F.mse_loss)
[ 0. 0.85056 0.83742]
[ 1. 0.79628 0.81775]
[ 2. 0.8012 0.80994]
What’s actually written in fastai library?
def get_emb(ni,nf):
e = nn.Embedding(ni, nf)
e.weight.data.uniform_(-0.05,0.05)
return e
class EmbeddingDotBias(nn.Module):
def __init__(self, n_factors, n_users, n_items, min_score, max_score):
super().__init__()
self.min_score,self.max_score = min_score,max_score
(self.u, self.i, self.ub, self.ib) = [get_emb(*o) for o in [
(n_users, n_factors), (n_items, n_factors), (n_users,1), (n_items,1)
]]
def forward(self, users, items):
um = self.u(users)* self.i(items)
res = um.sum(1) + self.ub(users).squeeze() + self.ib(items).squeeze()
return F.sigmoid(res) * (self.max_score-self.min_score) + self.min_score
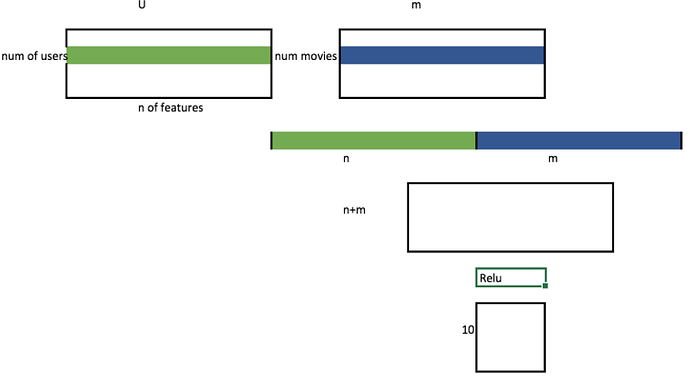
Let’s make a Neural Network (NN) version of this
Let’s look at the Excel.
All the users are compared to all movies.
Why not take the embedding and make a NN out of it?
Mini net
Let’s prototype our Embedding NN
-
(self.u, self.m) = [get_emb(*o) for o in..create embeddings -
nn.Linear(n_factors*2, 10, nh)- create our linear layers -
nhnumber of hidden layers -
torch.cat([self.u(users),self.m(movies)], dim=1)adds the two users and movies together -
F.relu(self.lin1(x)- linear
- relu 0, or Max; truncates negative values
- we have 1 layer, it is a NN, maybe not ‘deep’ per say
class EmbeddingNet(nn.Module):
def __init__(self, n_users, n_movies, nh=10):
super().__init__()
(self.u, self.m) = [get_emb(*o) for o in [
(n_users, n_factors), (n_movies, n_factors)]]
self.lin1 = nn.Linear(n_factors*2, 10, nh)
self.lin2 = nn.Linear(10, 1)
def forward(self, cats, conts):
users,movies = cats[:,0],cats[:,1]
x = F.dropout(torch.cat([self.u(users),self.m(movies)], dim=1), 0.75)
x = F.dropout(F.relu(self.lin1(x)), 0.75)
return F.sigmoid(self.lin2(x)) * (max_rating-min_rating+1) + min_rating-0.5
wd=5e-4
model = EmbeddingNet(n_users, n_movies).cuda()
opt = optim.SGD(model.parameters(), 1e-2, weight_decay=wd, momentum=0.9)
We will be using MSE loss as the optimizing metric
fit(model, data, 3, opt, F.mse_loss)
[ 0. 1.0879 1.10568]
[ 1. 0.81337 0.82665]
[ 2. 0.80449 0.79857]
Let’s explore the learning rate
set_lrs(opt, 1e-3)
fit(model, data, 3, opt, F.mse_loss)
[ 0. 0.68968 0.79054]
[ 1. 0.71873 0.78805]
[ 2. 0.70101 0.78719]
Neural Network Approach
- We can add dropouts
- we can use embeddings of different sizes
- we can add more hidden layers with more nodes
- we can add different amounts of regularization
Talk about the training loop
What’s happening inside?
opt = optim.SGD(model.parameters(), 1e-2, weight_decay=wd, momentum=0.9)
To the Excel!
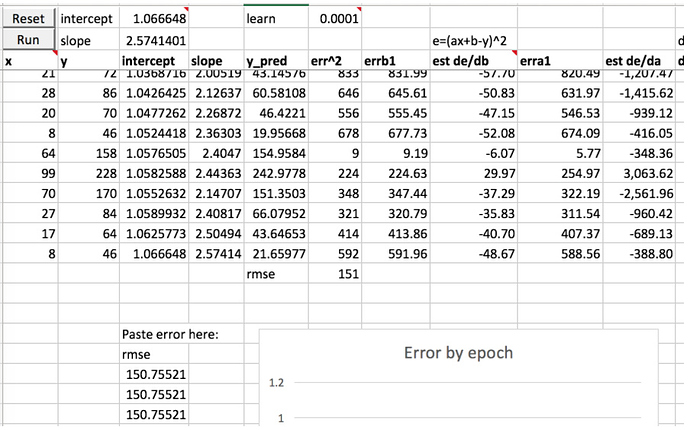
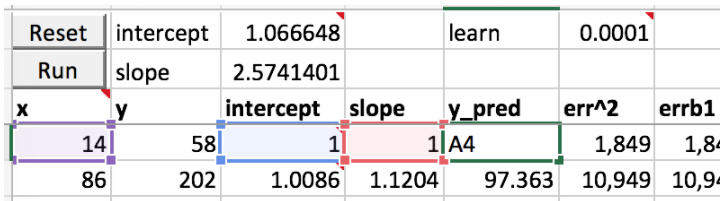
First create some data

Can we learn the slope and intercept?
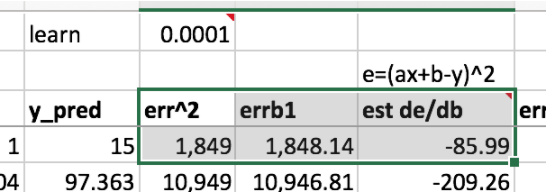
Lets look at the error equation (err^2=1,849)
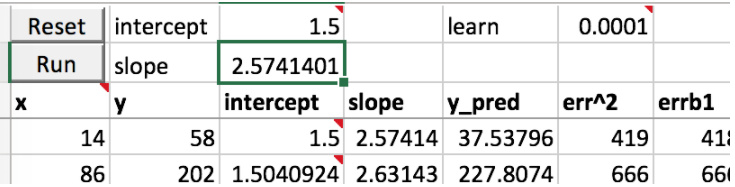
Increasing the intercept (1.5 up from 1) changes the error (err^2=419)
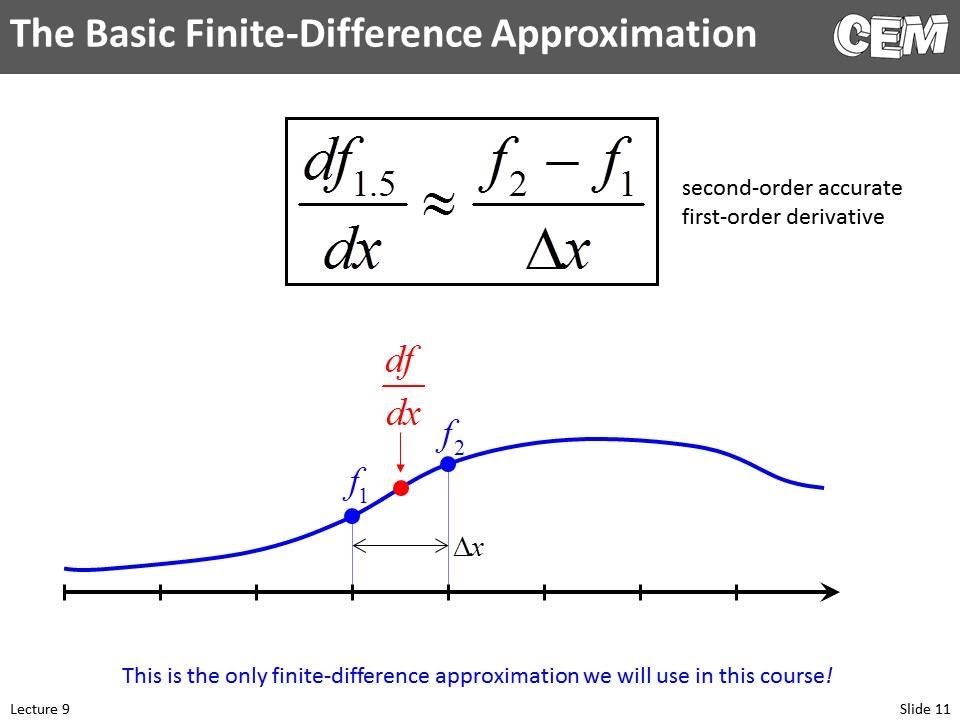
How can we guess where we should go next? Finite Differencing
A similar related term is back-propagation (the figure on the right)
Caveat: there’s a problem with finite differencing at high-dimensionality
1,000,000 ---> transformation ---> 100k
When you have a high dimensional space, your gradient becomes a huge matrix. The amount of calculation computation that you need is very high. Takes up a lot of memory, a lot of time.
Look up:
- Jacobian
- Hessian
More efficient: find the derivatives analytically instead of finite differencing.
Remember the chain rule from calculus (quick aside on how the chain rule works)
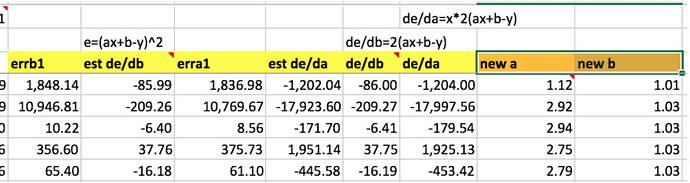
Explaining the manual calculation of the differentials, to calculate a new a and new b (orange), then run all back again.
Momentum: addressing how fast we come to a good solution
- Looking at SGD
de/da, we see that it is positive and negative at random. - The momentum idea is controlled by beta coefficients, will keep the differential going in the same direction, but a bit faster; will reduce the number of iterations.
- Adam is much much faster, but the answers are not as good as SGD with momentum.
- Recently, a newer version is out: AdamW that fixes weight decay issues. Ideally this will be fixed going forward.
About Adam Optimizer: even Faster!
Equals to our previous value of b, times learning rate divided by sqrt().
-
cellJ8= linear interpolation of derivative and the previous direction -
cellL8= linear interpolation of derivative squared + derivative squared from last step - this is also known as exponential weighted moving average
Some intuition on this (reminder, in the denominator)
- squared derivative is always positive
- if there’s a big change, the squared derivative will be huge
- so if there’s a big change, we divide the learning rate by a big number, (slow down)
- if there’s minimal change ( we will be more aggressive in choosing a new learning rate)
- adaptive learning rate - since the rate isn’t constant, but dependent the model’s optimization movements
Similar idea implemented in fastai libary
avg_loss = avg_loss * avg_mom + loss * (1-avg_mom)
From the fit function:
def fit(model, data, epochs, opt, crit, metrics=None, callbacks=None, **kwargs):
""" Fits a model
Arguments:
model (model): any pytorch module
net = to_gpu(net)
data (ModelData): see ModelData class and subclasses
opt: optimizer. Example: opt=optim.Adam(net.parameters())
epochs(int): number of epochs
crit: loss function to optimize. Example: F.cross_entropy
"""
stepper = Stepper(model, opt, crit, **kwargs)
metrics = metrics or []
callbacks = callbacks or []
avg_mom=0.98
batch_num,avg_loss=0,0.
for epoch in tnrange(epochs, desc='Epoch'):
stepper.reset(True)
t = tqdm(iter(data.trn_dl), leave=False, total=len(data.trn_dl))
for (*x,y) in t:
batch_num += 1
loss = stepper.step(V(x),V(y))
avg_loss = avg_loss * avg_mom + loss * (1-avg_mom) #<----------
debias_loss = avg_loss / (1 - avg_mom**batch_num)
t.set_postfix(loss=debias_loss)
stop=False
for cb in callbacks: stop = stop or cb.on_batch_end(debias_loss)
if stop: return
vals = validate(stepper, data.val_dl, metrics)
print(np.round([epoch, debias_loss] + vals, 6))
stop=False
for cb in callbacks: stop = stop or cb.on_epoch_end(vals)
if stop: break