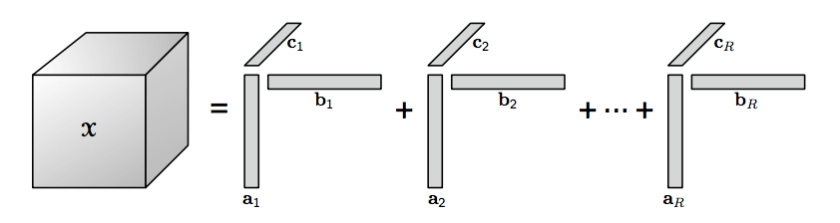
I am working on tensor decomposition and particularly PC Decomposition (preparing a blog post about how to compress CNNs and speed up their training). I am implementing the approach in Pytorch using autograd minimizing frobenius norm of diff of original and constructed tensor (basically L2 :|[X_tilde - X]|).
I went through many online sources and want to make sure my implementation is also valid, if anyone is fluent with this stuff.
The basic idea behind CP decomposition is that you define a rank R, then sum of outer product of rank 1 tensors is your approximation:
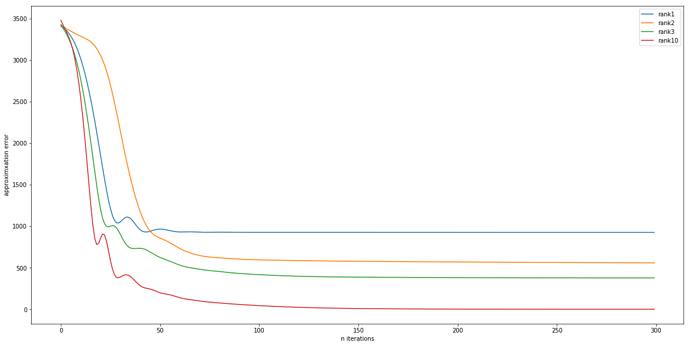
Actually I just crossed check my approximation error with tensorly which uses ALS (Alternating Least Squares) they are exactly the same with my Adam based optimization.
If anyone is interested here is the code:
def construct(A,B,C):
"""
Given Matrices A, B, C construct 3D Tensor
A : i, r
B: j, r
C : k, r
"""
X_tilde = 0
for i in range(r):
X_tilde += torch.ger(A[:,i], B[:,i]).unsqueeze(2)*C[:,i].unsqueeze(0).unsqueeze(0)
return X_tilde
def CP_decomposition(factors=[A,B,C], max_iter=10000, lr=0.1):
"""
Minimize Frobenius Norm |X-X_tilde|
Update decomposition factors
"""
opt = Adam(factors, lr=lr)
losses = []
for i in range(max_iter):
X_tilde = construct(*factors)
opt.zero_grad()
loss = torch.mean((X - X_tilde)**2)
#print(loss)
losses.append(loss.item())
loss.backward(retain_graph=True)
opt.step()
return losses
Decomposing a 3x4x5 tensor with Adam: