ML-Lecture 4.1
%load_ext autoreload
%autoreload 2
%matplotlib inline
import sys
# or wherever you have saved the repo
sys.path.append('/Users/tlee010/Desktop/github_repos/fastai/')
from fastai.imports import *
from fastai.structured import *
from pandas_summary import DataFrameSummary
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
from IPython.display import display
from sklearn import metrics
Discussion of combining Models
- Discussing the kaggle competition
- talking about strategies for improving scores, or improving top scoring kernels
Some Strategies
-
Average of different models (e.g. RF + GBM)
- Doesn’t work if one model is much worse than the other model
- other approach, the original group means model - calculate residuals
- then subtract the originals or divide by the original, and then use that as the target
- Multiplying different models: if the 2nd model targets teh ratio, you can predict the future ratios and then multiply the y_ratio vs. the y_answers
- Why does averaging works?
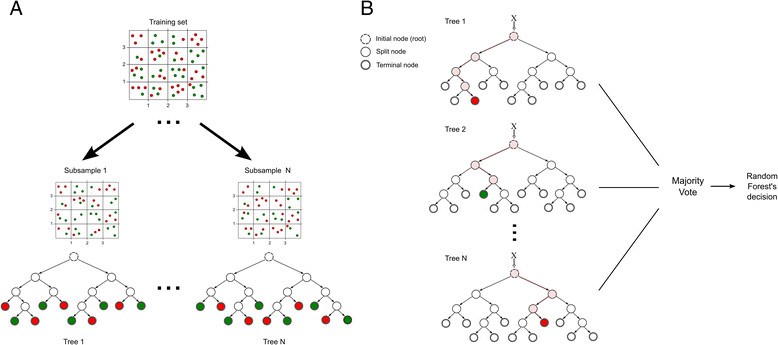
Illustration: Trees (in RF)
Each tree makes a prediction on a different set of data. With a large number of trees, ideally hoping that the sum of residuals will net to 0. This is also assuming that all the trees are comparably good systems.
Summary : What do we know about Random Forest?
Minimum
- Data you put in, needs to be numeric (convert dates to numbers)
- Strings into -> Categorical variables then into codes
- Missing values
Best practices
- Validation sets (not always a random sample)
- Know your metric (and optimize accordingly)
- Validation error based on the metric
Key Hyperparameters, make trees less good, but generalization improves
- Subsampling (
rf_samples) - Min_samples_leaf - limits when new leafs are made by setting a minimum point
- Max_features - 0.5 - choose random sample of features per split
Subsampling into different trees
Tree Size
If we have a large dataset, and we subset a dataset 20k. If we make a full tree (1 end node per row), then it will be log_2(20,000) deep. There are 20k leaf nodes. All the time of effort is usually put into the last layer of the random forest tree.
Can you have more than 1 record in a node?
If all the deciding variables are the same for more than 1 row, you would expect to have more than one row in one leaf.
Information Gain
We are trying to improve RMSE, or cross_entropy, whatever your loss function / scoring function, the ‘improvement’ is called information gain.
Repeat this process X times, for different subsets of 20k, each will be associated with its own trees
- Each tree has less levels (than overall)
- less nodes (less leafs ~ 20k instead of mil)
- Each tree is considered ‘weak’ because it is very good at its own subset
Two considerations for better Random Forests
- Each tree should be better
- between the trees, they should be less correlated. Otherwise the averaging effect will not reduce the error overall
Min_leaf_samples
If min leave samples = 2, what’s the number of leaf nodes? (half)
If min leave samples = 2, what’s the depth? log_2(20,000) - 1
Less trees, less processing, and better tree
HyperParameter
The parameters of a model are the actual values of the model. The actual data of the columns and Y. Hyper parameters are part of how we create the model. So an example would be processing iterations, or number of layers in a network etc. These help setup a model, but are not intrinsic to the observed data set.
Max Features
Max features will increase the randomness first. Withholding certain features will also prevent specific dominant features for prevailing over the tree.
Recapping Lesson1-RF
n_jobs - how many threads will be used on the random forest algorithm
oob - Everything that wasn’t in the sample, pull that out and use that to calculate the score. With multiple iterations, this serves as a validation set, and with enough subsets, all the rows should be eventually tested.

oob as an indicator
- if oob goes down, and validation goes down, that means overfitting
- if oob is fine, but validation goes down, then only the training dataset was affected. (When intermediate features were calculated and maybe were not applied to the training set)
** if you had 1 tree, with no replacement**
if you have few trees, some rows may not be pulled for the oob samples
be careful of large datasets and oob (since the non-sample dataset may be huge)
Sample Sizes
target a subset so that data will run very fast
- small enough that you can run in reasonable amount of time
- million+ use subsamples
- 100k don’t use it
Beyond Predictions - Confidence Intervals
Many times, we actually need to take an action. We need to retain customers, we need to figure out which accounts are high risk
Load Data
# loading the data (large)
#%time df_raw = pd.read_csv('/Users/tlee010/kaggle/bulldozers/Train.csv', low_memory=False, parse_dates=["saledate"])
# print('load complete')
Transform the data for modeling
# %%time
# train_cats(df_raw)
# add_datepart(df_raw, 'saledate')
# df_raw.saleYear.head()
# df_raw.SalePrice = np.log(df_raw.SalePrice)
Save for later
# df_raw.to_feather('/Users/tlee010/kaggle/bulldozers/bulldozers-raw')
import feather
df_raw = feather.read_dataframe('/Users/tlee010/kaggle/bulldozers/bulldozers-raw')
print('import complete')
import complete
Split and prep training sets
df_trn, y_trn, _ = proc_df(df_raw, 'SalePrice')
def split_vals(a,n): return a[:n], a[n:]
n_valid = 12000
n_trn = len(df_trn)-n_valid
X_train, X_valid = split_vals(df_trn, n_trn)
y_train, y_valid = split_vals(y_trn, n_trn)
raw_train, raw_valid = split_vals(df_raw, n_trn)
Setup our evaluation metrics
def rmse(x,y): return math.sqrt(((x-y)**2).mean())
def print_score(m):
res = [rmse(m.predict(X_train), y_train), rmse(m.predict(X_valid), y_valid),
m.score(X_train, y_train), m.score(X_valid, y_valid)]
if hasattr(m, 'oob_score_'): res.append(m.oob_score_)
print(res)
df_raw.head()
.dataframe thead th {
text-align: left;
}
.dataframe tbody tr th {
vertical-align: top;
}
| SalesID | SalePrice | MachineID | ModelID | datasource | auctioneerID | YearMade | MachineHoursCurrentMeter | UsageBand | fiModelDesc | ... | saleDay | saleDayofweek | saleDayofyear | saleIs_month_end | saleIs_month_start | saleIs_quarter_end | saleIs_quarter_start | saleIs_year_end | saleIs_year_start | saleElapsed | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1139246 | 11.097410 | 999089 | 3157 | 121 | 3.0 | 2004 | 68.0 | Low | 521D | ... | 16 | 3 | 320 | False | False | False | False | False | False | 1163635200 |
| 1 | 1139248 | 10.950807 | 117657 | 77 | 121 | 3.0 | 1996 | 4640.0 | Low | 950FII | ... | 26 | 4 | 86 | False | False | False | False | False | False | 1080259200 |
| 2 | 1139249 | 9.210340 | 434808 | 7009 | 121 | 3.0 | 2001 | 2838.0 | High | 226 | ... | 26 | 3 | 57 | False | False | False | False | False | False | 1077753600 |
| 3 | 1139251 | 10.558414 | 1026470 | 332 | 121 | 3.0 | 2001 | 3486.0 | High | PC120-6E | ... | 19 | 3 | 139 | False | False | False | False | False | False | 1305763200 |
| 4 | 1139253 | 9.305651 | 1057373 | 17311 | 121 | 3.0 | 2007 | 722.0 | Medium | S175 | ... | 23 | 3 | 204 | False | False | False | False | False | False | 1248307200 |
5 rows × 65 columns
Confidence based on tree variance
Recap: Feature importance - very key for finding top features
- Few features have most of the importance: Find only the feature importances over a certain threshold
- Collinearity distributes importance: random forests deal with collinearity very well, but one by-product is that collinear fields will ‘steal’ importance. The total importance will be distributed between the column.
- Feature filtering will consolidate importance: Feature importance filtering and recalculating will reconsolidate importance in the key fields
- We can also loop an shuffle columns and compare the performance with the column shuffled. It’s a good indicator for finding important features.
What if instead of shuffling approach. We built a tree with a single variable at a time, then measuring importance?
We would be missing out on interaction across multiple variables if we only looked at a single field at a time.
Feature Importance on the bulldozer set
set_rf_samples(50000)
m = RandomForestRegressor(n_estimators=40, min_samples_leaf=3, max_features=0.5, n_jobs=-1, oob_score=True)
m.fit(X_train, y_train)
print_score(m)
[0.20623327298398003, 0.24961117609288094, 0.91111012519736112, 0.88873052803450858, 0.89402299448247191]
%time preds = np.stack([t.predict(X_valid) for t in m.estimators_])
np.mean(preds[:,0]), np.std(preds[:,0])
CPU times: user 1.28 s, sys: 6.18 ms, total: 1.28 s
Wall time: 1.28 s
(9.262686293835575, 0.28751287842978079)
def get_preds(t): return t.predict(X_valid)
%time preds = np.stack(parallel_trees(m, get_preds))
np.mean(preds[:,0]), np.std(preds[:,0])
CPU times: user 66.6 ms, sys: 55.9 ms, total: 123 ms
Wall time: 415 ms
(9.262686293835575, 0.28751287842978079)
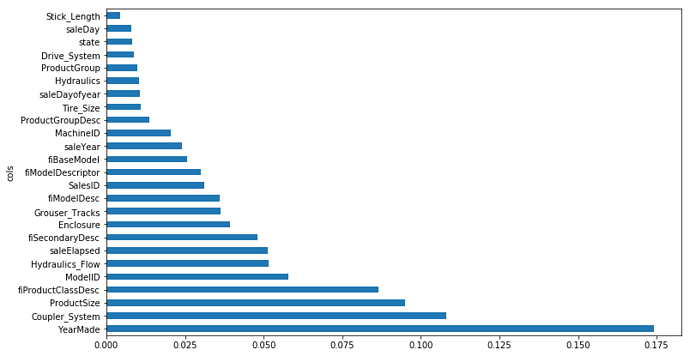
fi = rf_feat_importance(m, df_trn); fi[:10]
def plot_fi(fi): return fi.plot('cols', 'imp', 'barh', figsize=(12,7), legend=False)
plot_fi(fi[:30]);
Keep top features
to_keep = fi[fi.imp>0.005].cols; len(to_keep)
df_keep = df_trn[to_keep].copy()
X_train, X_valid = split_vals(df_keep, n_trn)
Retrain
m = RandomForestRegressor(n_estimators=40, min_samples_leaf=3, max_features=0.5,
n_jobs=-1, oob_score=True)
m.fit(X_train, y_train)
print_score(m)
[0.2069841382942022, 0.24614354845708988, 0.91046167671344647, 0.89180059105974052, 0.89411944174337954]
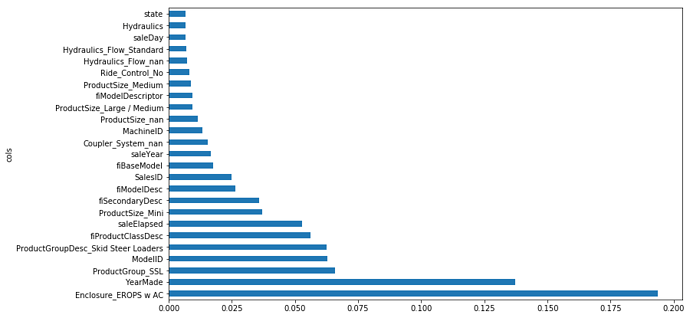
Re-examine the top features
fi = rf_feat_importance(m, df_keep)
plot_fi(fi);
One Hot Encoding
Given a single categorical field
High = 0
Low = 1
Med = 2
To find low, you would need to a lot of splits to find ‘Low’. As a field’s unique fields increase, the number of splits needed to find a specific category in single column will increase dramatically.
So instead we change them into fields. There is a trade-off between the number of fields being generated vs. how much processing you have made
max_n_cat = threshold before changing to one-hot encoding
df_trn2, y_trn, _ = proc_df(df_raw, 'SalePrice', max_n_cat=7)
X_train, X_valid = split_vals(df_trn2, n_trn)
m = RandomForestRegressor(n_estimators=40, min_samples_leaf=3, max_features=0.6, n_jobs=-1, oob_score=True)
m.fit(X_train, y_train)
print_score(m)
[0.20739388740281017, 0.2533820104194831, 0.91010682283162925, 0.8853432758769969, 0.89240567205245724]
fi = rf_feat_importance(m, df_trn2)
plot_fi(fi[:25]);
How can i reduce number of columns?
Spearman’s R - looking at ranking vs. a field see below
Convert everything to rank, then calculate the correlation coefficient
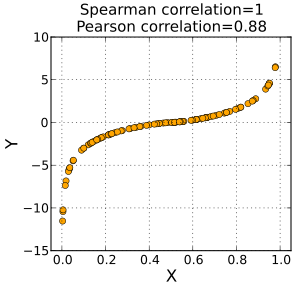
Removing redundant features
Fewer things to explain
One thing that makes this harder to interpret is that there seem to be some variables with very similar meanings. Let’s try to remove redundent features.
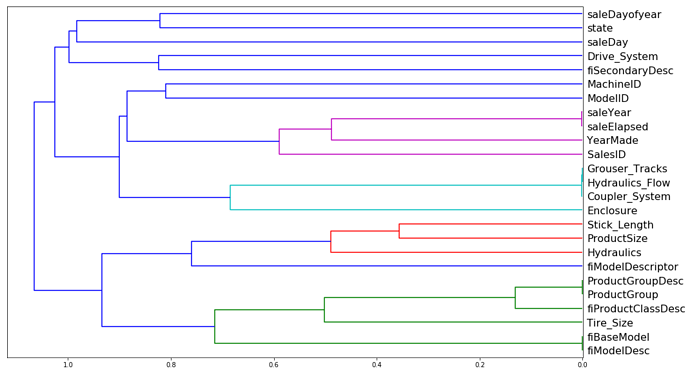
from scipy.cluster import hierarchy as hc
Iteratively compares columns together to see which fields are very close together. Will average them together and then compare the correlation to another field and then move up the hierarchy tree. This dendogram shows what fields may or may not be related
corr = np.round(scipy.stats.spearmanr(df_keep).correlation, 4)
corr_condensed = hc.distance.squareform(1-corr)
z = hc.linkage(corr_condensed, method='average')
fig = plt.figure(figsize=(16,10))
dendrogram = hc.dendrogram(z, labels=df_keep.columns, orientation='left', leaf_font_size=16)
plt.show()
Remove each redundant columns one at a time
def get_oob(df):
m = RandomForestRegressor(n_estimators=30, min_samples_leaf=5, max_features=0.6, n_jobs=-1, oob_score=True)
x, _ = split_vals(df, n_trn)
m.fit(x, y_train)
return m.oob_score_
Baseline
get_oob(df_keep)
0.89010697535232319
Loop, but loop and remove 1 of the similar pair
for c in ('saleYear', 'saleElapsed', 'fiModelDesc', 'fiBaseModel', 'Grouser_Tracks', 'Coupler_System'):
print(c, get_oob(df_keep.drop(c, axis=1)))
saleYear 0.889310279741
saleElapsed 0.887202486826
fiModelDesc 0.889103124363
fiBaseModel 0.889047474985
Grouser_Tracks 0.890271001016
Coupler_System 0.889396522484
Try dropping the fields
to_drop = ['saleYear', 'fiBaseModel', 'Grouser_Tracks']
get_oob(df_keep.drop(to_drop, axis=1))
0.88902644484599391
Seems to work, now try on the whole dataset (for another time )
df_keep.drop(to_drop, axis=1, inplace=True)
X_train, X_valid = split_vals(df_keep, n_trn)
Partial dependence
from pdpbox import pdp
from plotnine import *
import feather
df_raw = feather.read_dataframe('/Users/tlee010/kaggle/bulldozers/bulldozers-raw')
def split_vals(a,n): return a[:n], a[n:]
set_rf_samples(50000)
df_trn2, y_trn, _ = proc_df(df_raw, 'SalePrice', max_n_cat=7)
X_train, X_valid = split_vals(df_trn2, n_trn)
m = RandomForestRegressor(n_estimators=40, min_samples_leaf=3, max_features=0.6, n_jobs=-1)
m.fit(X_train, y_train);
plot_fi(rf_feat_importance(m, df_trn2)[:10]);
x_all = get_sample(df_raw[df_raw.YearMade>1930], 500)
from ggplot import ggplot
ggplot(x_all, aes('YearMade', 'SalePrice'))+stat_smooth(se=True, method='loess')
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
<ipython-input-51-b6295129bc7d> in <module>()
----> 1 ggplot(x_all, aes('YearMade', 'SalePrice'))+stat_smooth(se=True, method='loess')
~/anaconda/envs/fastai/lib/python3.6/site-packages/ggplot/ggplot.py in __init__(self, aesthetics, data)
54 self.data = data.copy()
55 self._handle_index()
---> 56 self.data = self._aes._evaluate_expressions(self.data)
57 self.data = self._aes.handle_identity_values(self.data)
58
AttributeError: 'aes' object has no attribute '_evaluate_expressions'
x = get_sample(X_train[X_train.YearMade>1930], 500)
def plot_pdp(feat, clusters=None, feat_name=None):
feat_name = feat_name or feat
p = pdp.pdp_isolate(m, x, feat)
return pdp.pdp_plot(p, feat_name, plot_lines=True,
cluster=clusters is not None, n_cluster_centers=clusters)
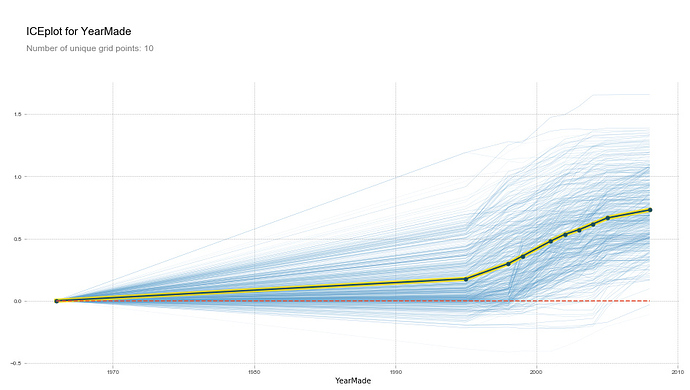
plot_pdp('YearMade')
(upload://dE3YhPzvJDRuI9s9RZjjqcKpufP.png)![output_62_0|690x390]
plot_pdp('YearMade', clusters=5)
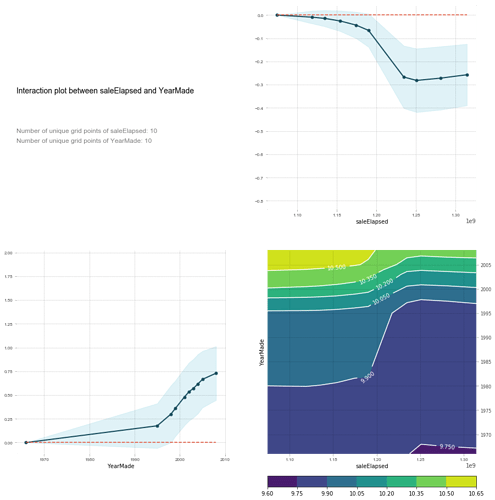
feats = ['saleElapsed', 'YearMade']
p = pdp.pdp_interact(m, x, feats)
pdp.pdp_interact_plot(p, feats)