[Maths Lesson 3] How does the summation range change with this substitution?

Part 1 (2017)
1

In http://colah.github.io/posts/2014-07-Understanding-Convolutions/ there are 2 equations separated by "If we substitute b=c−ab=c−a, we get "

I am confused how the range of summation changed from a + b = c to a. What I am able to understand is that a + b = c constrains the values. e.g. if c = 2 then a, b could be one of
(0, 2)
(1, 1)
(2, 0)

But a is a variable, so what does having that as range keep the equation same?

@amanmadaan In case you can help with the Maths.

2

Reading through the article further I can see that it was by visualization.

Another way that I was able to understand this was that the summation earlier was just a constrain over (a, b) as follows
a > 0
b > 0

This is needed because the distance will be positive.

Now as we replaced b by c - a we need to constrain (a, c - a)
a > 0
c - a (=b) > 0

We still have the constrain as the above can be written as c > a > 0. Probably just not written over the summation. But the constrain remains.

Just my thoughts in case someone gets stuck with same thing. Please feel free to add in case someone has anything to add.

3
  • Let’s look at a + b = c first.

“a” and “b” are the variables, and “c” is fixed.

It so happens that if you plot the set of all the points (a, b) that satisfy the equation above, you’ll get a line. For example, here is a + b = 50.

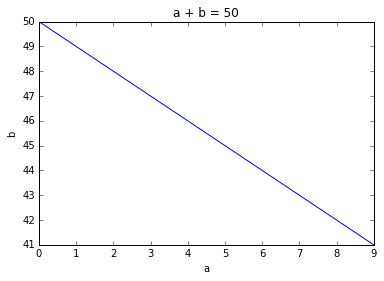
  • A summation over “a + b = c” simply means that you only want to include the points a, b that fall on this line. It’s thus enough that you iterate over the values of a and use c - a as the value of b.
2 Likes
4

Nice and easy to understand. Thanks.