After watching the lesson 9, I searched the underlying reason why we did the initialization that way. My research led me to the concept of variance of the random variables when they are added. Is this the case? Also I found a blog post explaining that concept in the linear algebra way. I want to build strong grasp on initialization techniques so can someone help me to understand if I am right and it is related to the variance of the random variables and also is blog post that I found is reliable and true?
Yes it is directly related to that concept, that is why you need to divide by the square root of the number of the nodes that activation is coming to make the variance 1 (because the number of weights is equal to that number, and variances add according to the sum of the variance of the random variables)
But I discovered that there might be a minor error in implementing kaiming in lecture 9 as the standard deviation of the uniform distribution is:
\sigma = \frac{b-a}{\sqrt{12}}
So as we scale the bounds with some scalar, we should do it in direct way not with square root as it directly affects standard deviation. Because of that, we should also adjust the gain function as it uses square root too.They can be modified as follows: (I am also tagging jeremy for possible minor error in the lecture @jeremy )
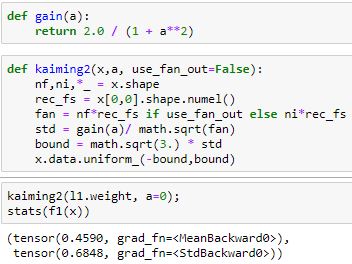
(before edit)
But in that lecture when we use uniform distribution for initialization we did the same thing and divide it by the square root of the number of nodes, but as far as I know, variance is added for normal distribution and I think we cannot say that for uniform distribution, variance will increase but I think it is not calculated by just adding the individual variances.
Before the last edit the quoted line was written in my answer but I realized that we can add the variances of the uniform distribution too as the expected value can be written as the mean of the distribution, so that is not a problem but I think we should not square root the gain part.