Huge valid_loss on tabular

[dzlob (David)]

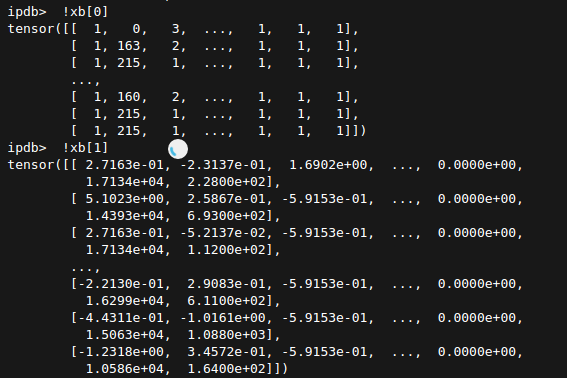
After upgrading to 1.0.40.dev0 from 1.0.39 something broke in my tabular learner.

The code works well on 1.0.39. But when launching it on 1.0.40.dev0, the following happens:

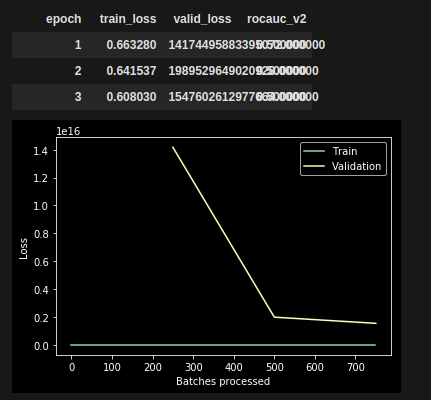
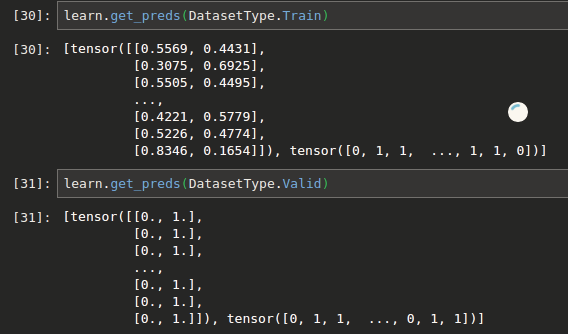
• train loss is calculated just fine, predictions seem reasonable
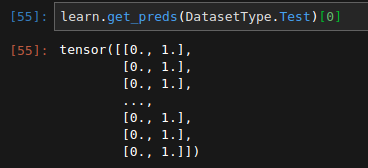
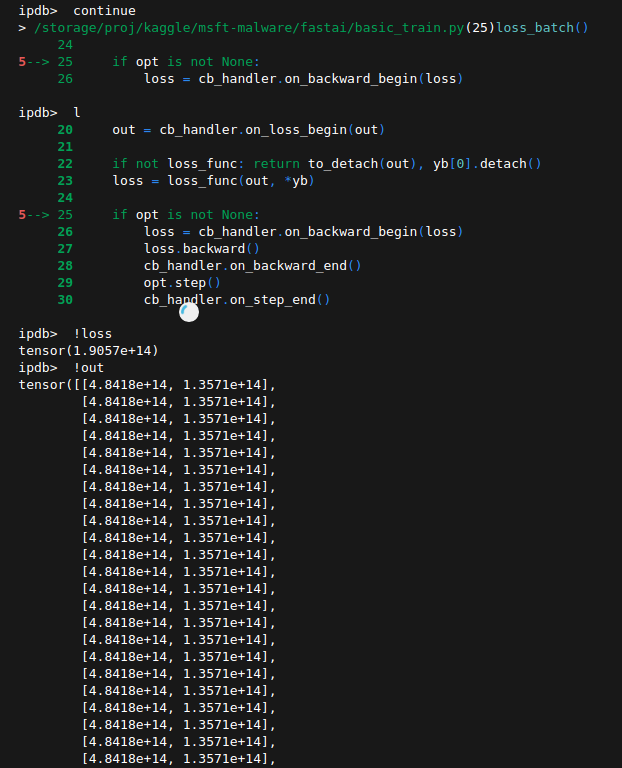
• validation loss explodes into millions. All predictions default to 1

I am having a hard time thinking of a hypothesis here.

Since Train and Validation come from the same dataframe, and predicted probs ALL become 1, while preds on train seem normal, I suspect there is some error with the library.

But at the same time, the tabular.ipynb example form github works just fine. So it must be something about my code/dataset that could cause this problem.

valid_idx = sorted(df.sample(frac=0.2, random_state=SEED).index)
test = TabularList.from_df(chunk.copy(), path='.', cat_names=cat_names, cont_names=cont_names)

src = TabularList.from_df(df.copy(), path='.', cat_names=cat_names, cont_names=cont_names, procs=procs) \
                           .split_by_idx(valid_idx) \
                           .label_from_df(cols=dep_var) \
                           .add_test(test)

original_data = src.databunch()

learn = tabular_learner(original_data, layers=[300, 100, 50], emb_szs=emb_szs, metrics=[rocauc_v2()], ps=[0.3, 0.3, 0.1], emb_drop=0.3)

learn.lr_find()
learn.recorder.plot()

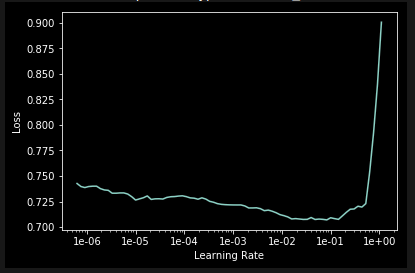
LR = 1e-03
learn.data.batch_size = 64

learn.fit_one_cycle(cyc_len=3, max_lr = LR)
learn.recorder.plot_losses()

[dzlob (David)]

I am trying to debug this problem.

All I’ve got so far, is that for some reason, all batches have these large predictions in out variable inside the loss_batch() function of basic_train.py

So let’s investigate where out gets these values.

See line 19,

out = model(*xb)

When comparing xb and yb in cases where loss was normal (train) and extremely high (validation) , I found this:

typical xb[1] stats for one batch with normal loss:

ipdb>  !xb[1].mean(), xb[1].min(), xb[1].max()
(tensor(-0.0181), tensor(-5.9664), tensor(5.7139))

typical xb[1] stats for one batch with huge loss:

ipdb>  !xb[1].mean(), xb[1].min(), xb[1].max()
(tensor(9.4444e+13), tensor(-1.9712), tensor(1.0000e+15))

ipdb>  !np.array(xb[1] > 100).mean()
0.6536458333333334

65% of values in xb[1] are unusually large (in a sample batch)

I’m still figuring out how we get to these xb and maybe my analysis is completely wrong.

[burgalon (Alon Burg)]

did you end up with any conclusion?